题目内容
18．
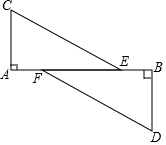如图，C、D分别位于路段A、B两点的正北处与正南处，现有两车分别从E、F两处出发，以相同的速度行驶，相同时间后分别到达C、D两地，休整一段时间后又以原来的速度行驶最终同时到达A、B两点，那么CE与DF平行吗？为什么？
分析 根据题意可得∠A=∠B=90°，AC=BD，CE=DF，然后再利用HL判定△AEC≌△BFD，进而可得结论．
解答 解：CE∥DF，
理由：由题意得，∠A=∠B=90°，
在Rt△AEC与Rt△BFD中，$\left\{\begin{array}{l}{CE=DF}\\{AC=BD}\end{array}\right.$，
∴Rt△AEC≌Rt△BFD，
∴∠AEC=∠BFD，
∴CE∥DF．
点评 此题主要考查了全等三角形的应用，关键是正确理解题意，找出证明三角形全等的条件．
练习册系列答案
阅读快车系列答案
相关题目
作图题（要求尺规作图，保留作图痕迹，不写作法）
9．一次函数y=kx+b过点（-2，5），且它的图象与y轴的交点和直线y=-$\frac{1}{2}$x-3与y轴的交点相同，那么一次函数的解析式是（ ）
| A． | y=-4x-3 | B． | y=-4x+3 | C． | y=4x-3 | D． | y=4x+3 |
如图，AC与BD相交于点E，AD∥BC，若AE：EC=1：2，则S△AED：S△CEB的值等于1：4．
3．下列说法正确的是（ ）
| A． | -$\frac{5}{3}$的倒数是$\frac{5}{3}$ | B． | -$\frac{2{x}^{2}y}{3}$的系数是$\frac{2}{3}$ | ||
| C． | -32的值是9 | D． | 3n-4m2n是三次二项式 |
10．
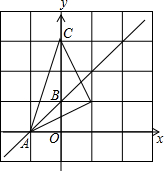如图，若△A′B′C′与△ABC关于直线AB对称，则点C的对称点C′的坐标是（ ）
如图，若△A′B′C′与△ABC关于直线AB对称，则点C的对称点C′的坐标是（ ）| A． | （0，1） | B． | （0，-3） | C． | （3，0） | D． | （2，1） |
