题目内容
13.观察下列各式:13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
猜想:13+23+33+…103=3025.
分析 由题意可知:从1开始的连续自然数的立方和等于这些数的和的平方,由此得出答案即可.
解答 解:∵13=12,
13+23=(1+2)2,
13+23+33=(1+2+3)2,
13+23+33+43=(1+2+3+4)2
…
∴13+23+33+…+103=(1+2+3+4+…+10)2=552=3025,
故答案为:3025.
点评 本题考查数字变化规律,观察出从1开始的连续自然数的立方和等于这些数的和的平方是解题的关键.

练习册系列答案
相关题目
1.下列单项式系数相同的是( )
①2x2 ②-2y2 ③$\frac{1}{2}$x2 ④2x3y4z.
①2x2 ②-2y2 ③$\frac{1}{2}$x2 ④2x3y4z.
| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③ |
8.收音机刻度盘上的波长λ和频率f的单位分别是米(m)和千赫兹(kHz),下面是波长λ和频率f的一些对应值:
(1)根据表中数据特征可判断频率f是波长λ的反比例函数(填“正比例”或“反比例”或“一次”),其表达式为f=$\frac{30000}{λ}$;
(2)当频率f不超过400kHz时,求波长λ(米)的取值范围.
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
(2)当频率f不超过400kHz时,求波长λ(米)的取值范围.

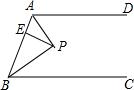 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为6.
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为6.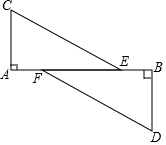 如图,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度行驶最终同时到达A、B两点,那么CE与DF平行吗?为什么?
如图,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度行驶最终同时到达A、B两点,那么CE与DF平行吗?为什么?