题目内容
15. 已知,如图,在△ABC中,∠BAC的外角平分线交CB的延长线于点E,求证:∠E=$\frac{1}{2}$(∠ABC-∠ACB)
已知,如图,在△ABC中,∠BAC的外角平分线交CB的延长线于点E,求证:∠E=$\frac{1}{2}$(∠ABC-∠ACB)
分析 根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠EAD和∠BAD,再根据角平分线的定义可得∠BAD=2∠EAD,然后整理即可得证.
解答 证明:由三角形的外角性质得,∠EAD=∠C+∠E,
∠BAD=∠C+∠ABC,
∵BE是∠BAC的外角平分线,
∴∠BAD=2∠EAD,
∴∠C+∠ABC=2(∠C+∠E),
∴∠E=$\frac{1}{2}$(∠ABC-∠ACB).
点评 本题考查了三角形的外角性质,主要利用了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
5.已知△ABC的三边长为a,b,c,且满足(a-2)2+|b-2|+|c-2|=0,则此三角形一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 一般三角形 |
 如图,△AEC≌△ADB,点E和点D为对应点,试说明(1)BE=CD;(2)∠DCO=∠EBO.
如图,△AEC≌△ADB,点E和点D为对应点,试说明(1)BE=CD;(2)∠DCO=∠EBO. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的是①②④.
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>2.其中正确的结论的是①②④.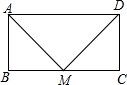 如图所示,矩形ABCD中,M是BC的中点,且MA⊥MD,若矩形的周长为36cm,求此矩形的面积.
如图所示,矩形ABCD中,M是BC的中点,且MA⊥MD,若矩形的周长为36cm,求此矩形的面积.