题目内容
向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0),若此炮弹在第6钞与第14秒时的高度相等,则炮弹达到最大高度的时间是( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
考点:二次函数的应用
专题:
分析:由于炮弹在第6s与第14s时的高度相等,即x取6和14时y的值相等,根据抛物线的对称性可得到抛物线y=ax2+bx的对称轴为直线x=6+
=10,然后根据二次函数的最大值问题求解
| 14-6 |
| 2 |
解答:
解:∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+
=10,
即炮弹达到最大高度的时间是10s.
故选:B.
∴抛物线y=ax2+bx的对称轴为直线x=6+
| 14-6 |
| 2 |
即炮弹达到最大高度的时间是10s.
故选:B.
点评:本题考查了二次函数的应用:先通过题意确定出二次函数的解析式,然后根据二次函数的性质解决问题;实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知等腰△ABC中,AD⊥BC于点D,且AD=
BC,则△ABC底角的度数为( )
| 1 |
| 2 |
| A、45°或75° |
| B、75° |
| C、45°或75°或15° |
| D、60° |
下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等.
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等.
| A、①②③ | B、③④⑤ |
| C、①②⑤ | D、②④⑤ |
 下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )
下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )A、 |
B、 |
C、 |
D、 |
 某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据: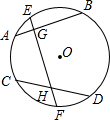 已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
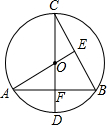 如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2
如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2