题目内容
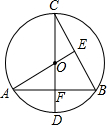 如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2
如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2| 2 |
(1)AB的长;
(2)⊙O的半径.
考点:垂径定理,勾股定理
专题:
分析:(1)连接AC,根据垂径定理求出BE=CE,AF=BF,根据线段垂直平分线性质求出AC=BC,AB=AC,求出AB=BC即可;
(2)求出∠BCD=30°和CE=
,解直角三角形求出即可.
(2)求出∠BCD=30°和CE=
| 2 |
解答:
解:(1)如图连接AC,
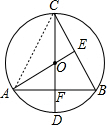
∵AO⊥BC,AO过O,
∴CE=BE,
∴AB=AC,
同理AC=BC,
∴AB=BC=2
;
(2)∵AB=BC=AC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵AC=BC,D⊥AB,
∴∠BCD=30°,
在Rt△CEO中,OC=
=
,
即⊙O的半径为
.

∵AO⊥BC,AO过O,
∴CE=BE,
∴AB=AC,
同理AC=BC,
∴AB=BC=2
| 2 |
(2)∵AB=BC=AC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵AC=BC,D⊥AB,
∴∠BCD=30°,
在Rt△CEO中,OC=
| CE |
| cos30° |
2
| ||
| 3 |
即⊙O的半径为
2
| ||
| 3 |
点评:本题考查了垂径定理,勾股定理,线段垂直平分线性质,等边三角形的性质和判定的应用,综合运用性质进行推理和计算是解此题的关键,综合性比较强,难度适中.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,是一个几何体的三视图,则这个几何体的形状是( )
如图,是一个几何体的三视图,则这个几何体的形状是( )| A、圆柱 | B、圆锥 | C、圆台 | D、长方体 |
向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0),若此炮弹在第6钞与第14秒时的高度相等,则炮弹达到最大高度的时间是( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
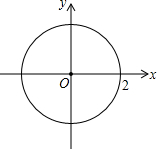 如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.
如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标. 如图,∠EOD=70°,射线OC,OB是∠EOA、∠DOA的角平分线.
如图,∠EOD=70°,射线OC,OB是∠EOA、∠DOA的角平分线. 如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC,△BCD的周长为13,求BC和ED的长.
如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC,△BCD的周长为13,求BC和ED的长.