题目内容
已知在△ABC中,∠ACB=90°,以△ABC的AB、AC为边向外作正方形ABDE、ACFG,连BG、CE、EG.
(1)探究CE与BG的关系;
(2)探究△ABC与△AEG面积是否仍然相等.
(1)探究CE与BG的关系;
(2)探究△ABC与△AEG面积是否仍然相等.
考点:全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质得出AG=AC,AB=AE,∠GAC=∠EAB=90°,求出∠GAB=∠CAE,推出△GAB≌△CAE即可;
(2)过E作EM⊥GA于M,根据正方形性质得出AE=AB,∠FCA=∠ACB=∠EAB=∠GAC=∠MAC=90°,求出∠EAM=∠CAB,证△AEM≌△ABC,推出BC=EM,根据三角形的面积公式求出即可.
(2)过E作EM⊥GA于M,根据正方形性质得出AE=AB,∠FCA=∠ACB=∠EAB=∠GAC=∠MAC=90°,求出∠EAM=∠CAB,证△AEM≌△ABC,推出BC=EM,根据三角形的面积公式求出即可.
解答: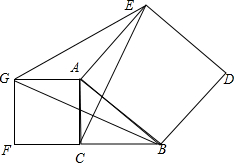 解:(1)CE=BG,
解:(1)CE=BG,
理由是:∵四边形ABDE、ACFG是正方形,
∴AG=AC,AB=AE,∠GAC=∠EAB=90°,
∴∠GAC+∠CAB=∠EAB+∠CAB,
∴∠GAB=∠CAE,
在△GAB和△CAE中,
∴△GAB≌△CAE(SAS),
∴CE=BG;
(2)△ABC与△AEG面积相等,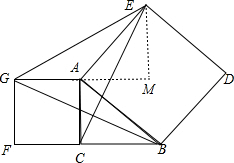
理由是:过E作EM⊥GA于M,
∵正方形AGFC和正方形ABDE,
∴AE=AB,∠FCA=∠ACB=∠EAB=∠GAC=∠MAC=90°,
∴∠EAM=∠CAB=90°-∠BAM,
在△AEM和△ABC中,
,
∴△AEM≌△ABC(AAS),
∴BC=EM,
∵S△ABC=
×AC×BC,S△AEG=
×AG×EM,
∴S△ABC=S△AEG,
即△ABC与△AEG面积相等.
 解:(1)CE=BG,
解:(1)CE=BG,理由是:∵四边形ABDE、ACFG是正方形,
∴AG=AC,AB=AE,∠GAC=∠EAB=90°,
∴∠GAC+∠CAB=∠EAB+∠CAB,
∴∠GAB=∠CAE,
在△GAB和△CAE中,
|
∴△GAB≌△CAE(SAS),
∴CE=BG;
(2)△ABC与△AEG面积相等,

理由是:过E作EM⊥GA于M,
∵正方形AGFC和正方形ABDE,
∴AE=AB,∠FCA=∠ACB=∠EAB=∠GAC=∠MAC=90°,
∴∠EAM=∠CAB=90°-∠BAM,
在△AEM和△ABC中,
|
∴△AEM≌△ABC(AAS),
∴BC=EM,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=S△AEG,
即△ABC与△AEG面积相等.
点评:本题考查了全等三角形的性质和判定,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等,解答(2)本题的关键是作出辅助线,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
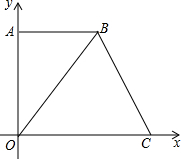 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.



