题目内容
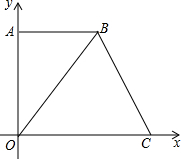 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.(1)求点B的坐标;
(2)点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H,设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(直接写出自变量t的取值范围).
考点:相似三角形的判定与性质,勾股定理
专题:
分析:(1)过点B作BN⊥OC,则四边形ABNO是矩形,BN=AO=8,AB=ON,由勾股定理可求得NB的长;
(2)可证△BON∽△POH,有
=
=
,由题意知OP=10-5t,OH=6-3tPH=8-4t,BH=OB-OH=10-(6-3t)=3t+4,从而求得S的表达式,由于OC=10,故0≤t<2.
(2)可证△BON∽△POH,有
| BO |
| PO |
| ON |
| OH |
| BN |
| PH |
解答: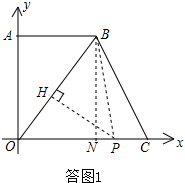 解:(1)如答图1,过点B作BN⊥OC,垂足为N
解:(1)如答图1,过点B作BN⊥OC,垂足为N
由题意知,OB=OC=10,BN=OA=8
∴ON=
=6,
∴B(6,8)
(2)如答图1,∵∠BON=∠POH,∠ONB=∠OHP=90°
∴△BON∽△POH,
∴
=
=
∵PC=5t,
∴OP=10-5t,
∴OH=6-3t,PH=8-4t,
∴BH=OB-OH=10-(6-3t)=3t+4,
∴S=
(3t+4)(8-4t)=-6t2+4t+16(0≤t<2).
 解:(1)如答图1,过点B作BN⊥OC,垂足为N
解:(1)如答图1,过点B作BN⊥OC,垂足为N由题意知,OB=OC=10,BN=OA=8
∴ON=
| OB2-BN2 |
∴B(6,8)
(2)如答图1,∵∠BON=∠POH,∠ONB=∠OHP=90°
∴△BON∽△POH,
∴
| BO |
| PO |
| ON |
| OH |
| BN |
| PH |
∵PC=5t,
∴OP=10-5t,
∴OH=6-3t,PH=8-4t,
∴BH=OB-OH=10-(6-3t)=3t+4,
∴S=
| 1 |
| 2 |
点评:本题主要考查了相似三角形的判定和性质,勾股定理、平面直角坐标系等知识点,解题的关键在于找到相似三角形,利用相似三角形的性质列出函数关系式.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O,且
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O,且