题目内容
在四边形ABCD中,对角线AC、BD相交于点O.
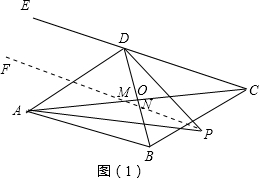
(1)如图(1),若∠BAC=∠ACD,∠AOB=70°,AP、DP分别平分∠BAC、∠BDC,求∠APD的度数;
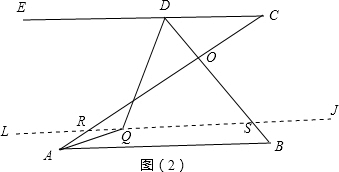
(2)如图(2),∠BAC=∠ACD,∠AOB=70°,DQ平分∠BDE,直线AQ平分∠BAC,求∠AQD的度数.

(1)如图(1),若∠BAC=∠ACD,∠AOB=70°,AP、DP分别平分∠BAC、∠BDC,求∠APD的度数;
(2)如图(2),∠BAC=∠ACD,∠AOB=70°,DQ平分∠BDE,直线AQ平分∠BAC,求∠AQD的度数.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)由条件可知AB∥CD,过P作PF∥AB,交AC、BD分别于点M、N,在△OMN中,由外角与平行的性质可求出∠APD的度数;
(2)方法类似(1).
(2)方法类似(1).
解答:解:(1)如图(1),过P作PF∥AB,交AC、BD分别于点M、N,
∵∠BAC=∠ACD,
∴AB∥CD,
∴PF∥CD,
∴∠FPA=∠BAP,∠FPD=∠PDC,
∵AP、DP分别是角平分线,
∴∠FPA=∠PAC,∠FPD=∠FPD,
∴∠OMN=2∠FPA,∠ONM=2∠FPD,
∵∠AOB=70°,
∴∠OMN+∠ONM=2∠FPA+2∠FPD=180°-70°=110°,
∴∠FPA+∠FPD=180°-70°=55°,
即∠APD=55°;
(2)如图(2),过Q作LJ∥AB,交AC于点R,交BD于点S,
∵∠BAC=∠ACD,
∴AB∥CD,
∴LJ∥CD,
∴∠LQA=∠BAQ,∠EDQ=∠DQJ,∠EDQ+∠LQD=180°,
∵AQ、DQ分别是角平分线,
∴∠BAQ=∠RAQ,∠SDQ=∠EDQ,
∴∠ORQ=2∠LQA,∠DSJ=2∠SQO,
∵∠DSJ=∠ORQ+∠AOB,
∴2∠SQD=2∠LQA+70°,
∴∠SQD-∠LQA=35°,
又∠AQD=∠LQA+LQD=∠LQA+180°-∠EDQ=180°-(∠DQE-∠LQA)=180°-35°=145°.

∵∠BAC=∠ACD,
∴AB∥CD,
∴PF∥CD,
∴∠FPA=∠BAP,∠FPD=∠PDC,
∵AP、DP分别是角平分线,
∴∠FPA=∠PAC,∠FPD=∠FPD,
∴∠OMN=2∠FPA,∠ONM=2∠FPD,
∵∠AOB=70°,
∴∠OMN+∠ONM=2∠FPA+2∠FPD=180°-70°=110°,
∴∠FPA+∠FPD=180°-70°=55°,
即∠APD=55°;
(2)如图(2),过Q作LJ∥AB,交AC于点R,交BD于点S,

∵∠BAC=∠ACD,
∴AB∥CD,
∴LJ∥CD,
∴∠LQA=∠BAQ,∠EDQ=∠DQJ,∠EDQ+∠LQD=180°,
∵AQ、DQ分别是角平分线,
∴∠BAQ=∠RAQ,∠SDQ=∠EDQ,
∴∠ORQ=2∠LQA,∠DSJ=2∠SQO,
∵∠DSJ=∠ORQ+∠AOB,
∴2∠SQD=2∠LQA+70°,
∴∠SQD-∠LQA=35°,
又∠AQD=∠LQA+LQD=∠LQA+180°-∠EDQ=180°-(∠DQE-∠LQA)=180°-35°=145°.
点评:本题主要考查平行线的判定和性质及三角形内角和定理,过点P和Q作平行线是解题的关键.

练习册系列答案
相关题目
为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,已知圆筒高108cm,其横截面周长为36cm,如果在表面缠绕油纸4圈,应裁剪多长油纸?( )
| A、90cm | B、180cm |
| C、135cm | D、120cm |
 如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )
如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )A、2-
| ||
B、2+
| ||
C、
| ||
D、
|
下列说法中,正确的是( )
| A、正有理数和负有理数统称有理数 |
| B、一个有理数不是整数就是分数 |
| C、零不是自然数,但它是有理数 |
| D、正分数、零、负分数统称分数 |
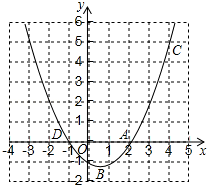 如图,已知二次函数y=ax2+bx+c的图象顶点是(
如图,已知二次函数y=ax2+bx+c的图象顶点是(