题目内容
2．
如图，在△ABC中，∠A=60°，∠C=70°，点O是△ABC的内心，BO的延长线交AC于点D，求∠BDC的度数．
分析 先根据内心的定义得到∠DBC=$\frac{1}{2}$∠ABC，再利用三角形内角和是180度求解即可．
解答 解：∵∠A=60°，∠C=70°，
∴∠ABC=50°，
∵点O为△ABC的内心，
∴∠DBC=$\frac{1}{2}$∠ABC=25°，
∵∠ACB=78°，∠DBC+∠C+∠BDC=180°，
∴∠BDC=180°-78°-25°=77°．
点评 本题考查了三角形的内切圆与内心，三角形的内角和，角平分线的定义，熟练掌握三角形的 角平分线的定义是解题的关键．
练习册系列答案
相关题目
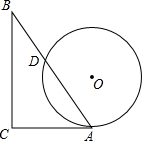如图，一个含有30°角的直角三角板ABC的直角边AC与⊙O相切于点A，∠C=90°，∠B=30°，⊙O的直径为4，AB与⊙O相交于D点，则AD的长为2$\sqrt{3}$．
如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D为边CB上的一个动点（点D不与点B重合），过D作DE⊥AB，垂足为E，点B′在边AB上，且与点B关于直线DE对称，连接CB′，当△AB′C为等腰三角形时，BD的长$\frac{5}{2}$或$\frac{7}{4}$或$\frac{25}{8}$．
已知反比例函数y=$\frac{5-m}{x}$（m为常数）的图象经过点A（1，6）．
7．下列四个手机APP图标中，是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
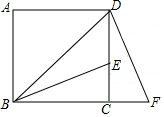如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC与点E，将△BCE绕点C按顺时针旋转90°得到△DCF，若CE=3cm，则FB=（6+3$\sqrt{2}$）cm．
如图，A，B是平面上的两定点，在平面上找一点C，使△ABC为等腰直角三角形，且点C为直角顶点，这样的点C有几个？