题目内容
14.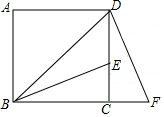 如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C按顺时针旋转90°得到△DCF,若CE=3cm,则FB=(6+3$\sqrt{2}$)cm.
如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C按顺时针旋转90°得到△DCF,若CE=3cm,则FB=(6+3$\sqrt{2}$)cm.
分析 过点E作EM⊥BD于点M,则△DEM为等腰直角三角形,根据角平分线以及等腰直角三角形的性质即可得出DE的长度,再根据正方形以及旋转的性质,即可得出线段BF的长.
解答 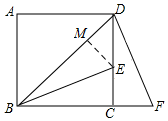 解:如图所示,过点E作EM⊥BD于点M.
解:如图所示,过点E作EM⊥BD于点M.
∵四边形ABCD为正方形,
∴∠BAC=45°,∠BCD=90°,
∴△DEM为等腰直角三角形.
∵BE平分∠DBC,EM⊥BD,EC⊥BC,
∴EM=EC=3,
∴DE=$\sqrt{2}$EM=3$\sqrt{2}$,
∴BC=CD=3$\sqrt{2}$+3.
由旋转的性质可知:CF=CE=3,
∴BF=BC+CF=3$\sqrt{2}$+3+3=6+3$\sqrt{2}$.
故答案为:6+3$\sqrt{2}$.
点评 本题考查了旋转的性质、正方形的性质以及角平分线的性质,解题的关键是结合角平分线以及等腰直角三角形的性质,求出线段BC以及CF的长度.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.掷一枚质地均匀的骰子,下列事件是不可能事件是( )
| A. | 向上一面点数是奇数 | B. | 向上一面点数是偶数 | ||
| C. | 向上一面点数是大于6 | D. | 向上一面点数是小于7 |
9.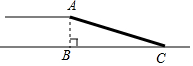 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.| A. | 16 | B. | 10 | C. | 18 | D. | 8$\sqrt{3}$ |
 如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.
如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数. 如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.
如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.