题目内容
13.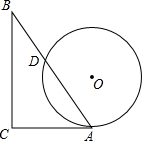 如图,一个含有30°角的直角三角板ABC的直角边AC与⊙O相切于点A,∠C=90°,∠B=30°,⊙O的直径为4,AB与⊙O相交于D点,则AD的长为2$\sqrt{3}$.
如图,一个含有30°角的直角三角板ABC的直角边AC与⊙O相切于点A,∠C=90°,∠B=30°,⊙O的直径为4,AB与⊙O相交于D点,则AD的长为2$\sqrt{3}$.
分析 连接OA、过O作OE⊥AD于E,根据垂径定理求出AD=2AE,根据切线性质求出∠OAC=90°,求出∠OAE=30°,即可求出AE,即可求出答案.
解答 解: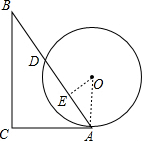
连接OA、过O作OE⊥AD于E,
∵在Rt△BCA中,∠C=90°,∠B=30°,
∴∠BAC=60°,
∵⊙O切AC于A,
∴∠OAC=90°,
∴∠OAE=30°,
∵OA=2,
∴OE=1,OA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵OE⊥AD,OE过O,
∴AD=2AE=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查了垂径定理和切线的性质、勾股定理、含30°角的直角三角形性质等知识点,能正确作出辅助线是解此题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5.掷一枚质地均匀的骰子,下列事件是不可能事件是( )
| A. | 向上一面点数是奇数 | B. | 向上一面点数是偶数 | ||
| C. | 向上一面点数是大于6 | D. | 向上一面点数是小于7 |
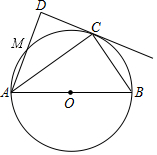 如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.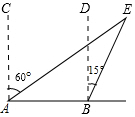 如图,一艘船上午9时在A处望见灯塔E在北偏东60°方向上,此船沿正东方向以每小时30海里的速度航行,11时到达B处,在B处测得灯塔E在北偏东15°方向上.
如图,一艘船上午9时在A处望见灯塔E在北偏东60°方向上,此船沿正东方向以每小时30海里的速度航行,11时到达B处,在B处测得灯塔E在北偏东15°方向上.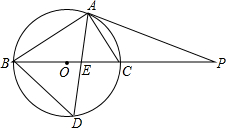 如图,已知⊙O中,PA切⊙O于A,PB过圆心且与圆交于点C,D为$\widehat{BC}$中点,AD交BC于E,若AB=8,tan∠ABC=$\frac{3}{4}$.
如图,已知⊙O中,PA切⊙O于A,PB过圆心且与圆交于点C,D为$\widehat{BC}$中点,AD交BC于E,若AB=8,tan∠ABC=$\frac{3}{4}$. 如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.
如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.