题目内容
12.如图所示的玩具,其主要部分是由六个全等的菱形组成,菱形边长为3cm,现将玩具尾部点B1固定,当这组菱形形状发生变化时,玩具的头部B1沿射线移动.(1)当∠A1B1C1=120°时,求B1,B7两点间的距离.
(2)当∠A1B1C1由120°变为60°时,点B1移动了多少cm?

分析 (1)连结B1B2,根据菱形的性质可得△B1A1B2是等边三角形,根据等边三角形的性质可得B1B2=3cm,根据全等的性质即可求解;
(2)连结B1B2,根据菱形的性质可得△B1A1B2是顶角为120°的等腰三角形,根据等腰三角形的性质可得B1B2=3$\sqrt{3}$cm,根据全等的性质即可求解.
解答 解:(1)连结B1B2,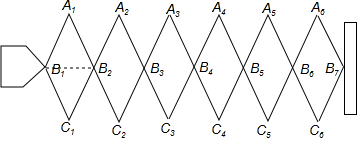 ∵四边形A1B1C1B2是菱形,
∵四边形A1B1C1B2是菱形,
∴A1B1=A1B2,C1B1∥A1B2,
∵∠A1B1C1=120°,
∴∠B1A1B2=60°,
∴△B1A1B2是等边三角形,
∴B1B2=B1A1,
∵B1A1=3cm,
∴B1B2=3cm,
∵六个菱形均全等,
∴B1B7=18cm;
(2)连结B1B2,
∵四边形A1B1C1B2是菱形,
∴A1B1=A1B2,C1B1∥A1B2,
∵∠A1B1C1=60°,
∴∠B1A1B2=120°,
∴△B1A1B2是顶角为120°的等腰三角形,
∴B1B2=$\sqrt{3}$B1A1,
∵B1A1=3cm,
∴B1B2=3$\sqrt{3}$cm,
∵六个菱形均全等,
∴B1B7=18$\sqrt{3}$cm,
∴B1移动了(18$\sqrt{3}$-18)cm.
点评 考查了菱形的性质,等边三角形的判定与性质可得B1B2=3cm,等腰三角形判定与性质,全等的性质,关键是得到B1B7的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在反比例函数y=$\frac{k}{x}$(k<0)的图象上有两点(-1,y1),($\frac{1}{4}$,y2),则y1-y2的值是( )
| A. | 负数 | B. | 非正数 | C. | 正数 | D. | 不能确定 |
2.正比例函数的图象经过点(-1,2),则这个图象必须经过点( )
| A. | (-2,1) | B. | (2,-1) | C. | (1,-2) | D. | (1,2) |
 如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.
如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数. 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.