题目内容
17. 已知反比例函数y=$\frac{5-m}{x}$(m为常数)的图象经过点A(1,6).
已知反比例函数y=$\frac{5-m}{x}$(m为常数)的图象经过点A(1,6).(1)求m的值;
(2)如图,过点A作直线AC与函数y=$\frac{5-m}{x}$的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
分析 (1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;
(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,则△CBD∽△CAE,运用相似三角形知识求出CD的长即可求出点C的横坐标.
解答 解:(1)∵图象过点A(1,6),
∴$\frac{5-m}{1}$=6,
解得m=-1.
故m的值为-1;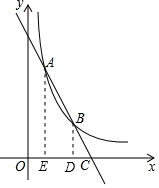 (2)分别过点A、B作x轴的垂线,垂足分别为点E、D,
(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,
由题意得,AE=6,OE=1,即A(1,6),
∵BD⊥x轴,AE⊥x轴,
∴AE∥BD,
∴△CBD∽△CAE,
∴$\frac{CB}{CA}$=$\frac{BD}{AE}$,
∵AB=2BC,
∴$\frac{CB}{CA}$=$\frac{1}{3}$,
∴$\frac{1}{3}$=$\frac{BD}{6}$,
∴BD=2.
即点B的纵坐标为2.
当y=2时,x=3,即B(3,2),
设直线AB解析式为:y=kx+b,
把A和B的坐标代入得:$\left\{\begin{array}{l}{k+b=6}\\{3k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$,
∴直线AB解析式为y=-2x+8,
令y=0,解得x=4,
∴C(4,0).
点评 此题考查了待定系数法求函数的解析式以及反比例函数与一次函数的交点问题.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
5.掷一枚质地均匀的骰子,下列事件是不可能事件是( )
| A. | 向上一面点数是奇数 | B. | 向上一面点数是偶数 | ||
| C. | 向上一面点数是大于6 | D. | 向上一面点数是小于7 |
9.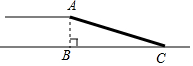 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.| A. | 16 | B. | 10 | C. | 18 | D. | 8$\sqrt{3}$ |
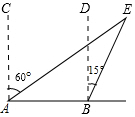 如图,一艘船上午9时在A处望见灯塔E在北偏东60°方向上,此船沿正东方向以每小时30海里的速度航行,11时到达B处,在B处测得灯塔E在北偏东15°方向上.
如图,一艘船上午9时在A处望见灯塔E在北偏东60°方向上,此船沿正东方向以每小时30海里的速度航行,11时到达B处,在B处测得灯塔E在北偏东15°方向上.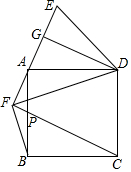 如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.
如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE. 如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.
如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.