题目内容
3.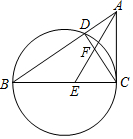 如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC,E是BC上一点,AE与CD交于点F,若BE=6,tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,则圆的直径是10,$\frac{AF}{FE}$=$\frac{10}{9}$.
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC,E是BC上一点,AE与CD交于点F,若BE=6,tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,则圆的直径是10,$\frac{AF}{FE}$=$\frac{10}{9}$.
分析 作EM⊥AB于M,根据tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,求出EC、BC与AC的关系,再根据BC-EC-BE=6,列出方程求出AC,由此即可求出直径,第二个问题注意求出AD:BD、DM:BD的值即可解决问题.
解答 解:∵BC是直径,
∴∠BDC=90°,
∵∠ABC+∠BCD=90°,∠ACD=∠ABC,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{2}{3}$,tan∠AEC=$\frac{AC}{EC}$=$\frac{5}{3}$,
∴EC=$\frac{3}{5}$AC,BC=$\frac{3}{2}$AC,
∵BC-EC=BE=6,
∴$\frac{3}{2}$AC-$\frac{3}{5}$AC=6,
∴AC=$\frac{20}{3}$,
∴BC=$\frac{3}{2}$×$\frac{20}{3}$=10.
作EM⊥AB于M,
∵∠CAD=∠CBA,∠BCA=∠CDA,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,
∴AD=$\frac{A{C}^{2}}{AB}$,同理BD=$\frac{B{C}^{2}}{AB}$,
∴$\frac{AD}{BD}$=$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{4}{9}$,
∴AD=$\frac{4}{9}$BD,
∵EM∥CD,
∴$\frac{DM}{BD}$=$\frac{EC}{CB}$,
∴DM=$\frac{2}{5}$BD,
∵EM∥DF,
∴$\frac{AF}{EF}$=$\frac{AD}{DM}$=$\frac{10}{9}$.
故答案分别为10,$\frac{10}{9}$
点评 本题考查相似三角形、圆周角定理、解直角三角形、平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识.属于中考常考题型

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案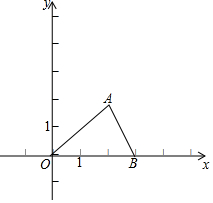 如图:A,B两点的坐标分别是(2,$\sqrt{3}$),(3,0).
如图:A,B两点的坐标分别是(2,$\sqrt{3}$),(3,0).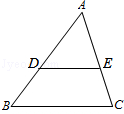 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.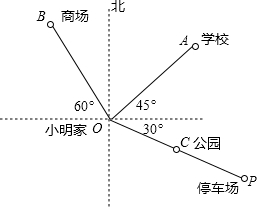 如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.
如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.