题目内容
12.观察下列算式:1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
…
按规律填空:
(1)1+3+5+7+9=52;
(2)1+3+5+…+2005=10032.
(3)1+3+5+7+9+…+2n-1=n2
(4)根据以上规律计算101+103+105+…+499.
分析 观察数据可知,规律是:等号右边的数是等号左边首数与末数的平均数的平方.根据规律解题即可.
解答 解:(1)1+3+5+7+9=25=52,
(2)1+3+5+…+2005=10032,
(3)1+3+5+7+9+…+(2n-1)=n2
(4)101+103+105+…+497+499=(101+499)×200÷2=60000.
故答案为:(1)52;(2)10032(3)2n-1.
点评 此题主要考查了数字变化规律,得出从奇数1开始,连续奇数的和等于数的个数的平方是解题关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
4. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
2.下列运算错误的是( )
| A. | 3a•(-2a)2=12a3 | B. | 3x4-x4=2x4 | C. | xy4÷(-xy)=-xy3 | D. | -(2x3y2)3=-8x9y6 |
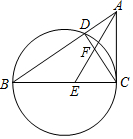 如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC,E是BC上一点,AE与CD交于点F,若BE=6,tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,则圆的直径是10,$\frac{AF}{FE}$=$\frac{10}{9}$.
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC,E是BC上一点,AE与CD交于点F,若BE=6,tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,则圆的直径是10,$\frac{AF}{FE}$=$\frac{10}{9}$. 已知,如图,直角△ABC中,∠C=90°
已知,如图,直角△ABC中,∠C=90° 如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.
如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.