题目内容
2. 如图,在△ABC中,AD平分∠BAC,∠ABC=2∠ACB,过BC中点M作AD垂线,交AD、AB的延长线于F、E,过点C作CQ∥ME交AB延长线于点Q.
如图,在△ABC中,AD平分∠BAC,∠ABC=2∠ACB,过BC中点M作AD垂线,交AD、AB的延长线于F、E,过点C作CQ∥ME交AB延长线于点Q.(1)若∠ABC=60°,AB=2,求EM的长;
(2)求证:BE=$\frac{1}{2}$BD.
分析 (1)如图1中,首先证明△ABC是直角三角形,求出AQ、AC、QC,根据三角形中位线定理即可求出EM.
(2)如图2中,连接QD,延长AF交QC于H.首先证明△AQD≌△ACD,推出AQ=AC,∠AQD=∠ACB,只要证明BQ=BD,BE=EQ即可解决问题.
解答 解:(1)如图1中,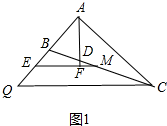
∵∠ABC=2∠ACB,∠ABC=60°,
∴∠ACB=30°,∠BAC=90°,
∵AB=2,
∴BC=2AB=4,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=2$\sqrt{3}$,
∵∠EAF=∠CAF=45°,AF⊥EF,
∴∠AEF=45°,
∵QC∥EM,
∴∠Q=∠AEF=45°,
∴∠Q=∠ACQ=45°,
∴AQ=AC=2$\sqrt{3}$,
∴QC=$\sqrt{A{Q}^{2}+A{C}^{2}}$=2$\sqrt{6}$,
∵BM=MC,EM∥CQ,
∴BE=EQ,
∴EM=$\frac{1}{2}$CQ=$\sqrt{6}$.
(2)如图2中,连接QD,延长AF交QC于H.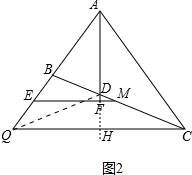
∵EM∥QC⊥EM,
∴AH⊥QC,
∵∠HAQ=∠HAC,
∠HAQ+∠AQH=90°,∠HAC+∠ACH=90°,
∴∠AQC=∠ACQ,
∴AQ=AC,
∵AD=AD,∠QAD=∠CAD,AQ=QC,
∴△AQD≌△ACD,
∴∠AQD=∠ACB,
∵∠ABC=∠AQD+∠BDQ=2∠ACB=2∠AQD,
∴∠BQD=∠BDQ,
∴BD=BQ,
∵BM=MC,EM∥CQ,
∴EB=EQ,
∴BD=2BE,即BE=$\frac{1}{2}$BD.
点评 本题考查全等三角形的判定和性质、勾股定理、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
12. 如图,在菱形ABCD中,过点A作AE⊥BC,BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为( )
如图,在菱形ABCD中,过点A作AE⊥BC,BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为( )
 如图,在菱形ABCD中,过点A作AE⊥BC,BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为( )
如图,在菱形ABCD中,过点A作AE⊥BC,BC于点E,若菱形ABCD的面积为24,AE=4,则AB的长为( )| A. | 12 | B. | 6 | C. | $\sqrt{13}$ | D. | 2$\sqrt{13}$ |
13.为了解初中生的健康状况,相关部分随机抽取了某校的部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分,请根据图表信息回答下列问题:

(1)表中a=45%,b=15%,本次共抽取了多少名学生进行测试?
(2)扇形图中区域B所对应的扇形圆心角的度数为162°;
(3)若该校有2000名学生,请估计成绩为优秀或良好的学生人数.
| 组别 | 测试成绩 | 百分比 |
| A | 优秀 | 10% |
| B | 良好 | a |
| C | 及格 | 30% |
| D | 不及格 | b |

(1)表中a=45%,b=15%,本次共抽取了多少名学生进行测试?
(2)扇形图中区域B所对应的扇形圆心角的度数为162°;
(3)若该校有2000名学生,请估计成绩为优秀或良好的学生人数.
17.用配方法解下列方程,配方正确的是( )
| A. | x2+6x-7=0可化为(x+3)2=2 | B. | x2-2x-9=0可化为(x-1)2=8 | ||
| C. | x2+8x-9=0可化为(x+4)2=16 | D. | x2-4x=0可化为(x-2)2=4 |
7.下列调查中,适宜采用全面调查的是( )
| A. | 了解我省中学生的视力情况 | B. | 了解九(1)班学生校服的尺码情况 | ||
| C. | 检测一批电灯泡的使用寿命 | D. | 调查《体育新闻》栏目的收视率 |
11.如果关于x的一元二次方程mx2+4x-1=0没有实数根,那么m的取值范围是( )
| A. | m<4且m≠0 | B. | m<-4 | C. | m>-4且m≠0 | D. | m>4 |
 如图,正方形ABCD的边长为4$\sqrt{5}$,E、F分别是AB、BC的中点,动点G从D点出发沿DE以每秒1个单位的速度向E点运动,设运动时间为t秒,当∠EGF=45°时,求t的值.
如图,正方形ABCD的边长为4$\sqrt{5}$,E、F分别是AB、BC的中点,动点G从D点出发沿DE以每秒1个单位的速度向E点运动,设运动时间为t秒,当∠EGF=45°时,求t的值.