题目内容
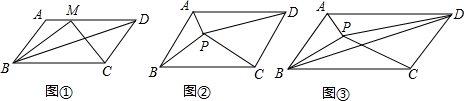
如图，已知AB∥CD，∠1=∠2，你能判断AE∥DF吗？说说你的理由．考点：平行线的判定与性质
专题：常规题型
分析：根据平行线的性质由AB∥CD得∠CDA=∠BAD，加上∠1=∠2，利用等式的性质可得到∠FDA=∠EAD，然后根据平行线的判定即可得到AE∥DF．
解答：解：能判断AE∥DF．
理由如下：
∵AB∥CD，
∴∠CDA=∠BAD，
而∠1=∠2，
∴∠CAD-∠1=∠BAD-∠2，
即∠FDA=∠EAD，
∴AE∥DF．
理由如下：
∵AB∥CD，
∴∠CDA=∠BAD，
而∠1=∠2，
∴∠CAD-∠1=∠BAD-∠2，
即∠FDA=∠EAD，
∴AE∥DF．
点评：本题考查了平行线的判定与性质：内错角相等，两直线平行；两直线平行，内错角相等．
练习册系列答案
相关题目
若a＞b，则下列不等式正确的是（ ）
| A、2a＜2b | ||||
| B、a-2＞b-2 | ||||
C、-
| ||||
| D、a-b＜0 |
若n≠0，a＜b，则下列不等式中成立的是（ ）
| A、an＜bn | ||||
| B、an2＜bn2 | ||||
C、
| ||||
D、-
|
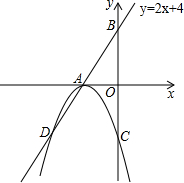如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，-4）．
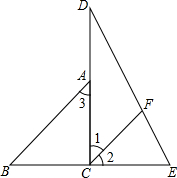将一副三角板拼成如图的图形，其中CD⊥BE于点C，∠D=30°，∠B=45°，且过点C作CF平分∠DCE交DE于点F．
如图，已知正方形ABCD的边长是2，∠EAF=m°，将∠EAF绕点A顺时针旋转，它的两边分别交BC、CD于点E、F，G是CB延长线上一点，且始终保持BG=DF．