题目内容
我们知道:平行四边形的面积=(底边)×(这条底边上的高).如图,四边形ABCD都是平行四边形,AD∥BC,AB∥CD,设它的面积为S.
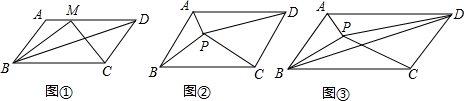
(1)如图①,点M为AD上任意一点,若△BCM的面积为S1,则S1:S= ;
(2)如图②,点P为平行四边形ABCD内任意一点时,记△PAB的面积为Sˊ,△PCD的面积为S〞,平行四边形ABCD的面积为S,猜想得Sˊ、S〞的和与S的数量关系式为 ;
(3)如图③,已知点P为平行四边形ABCD内任意一点,△PAB的面积为3,△PBC的面积为7,求△PBD的面积.
(1)如图①,点M为AD上任意一点,若△BCM的面积为S1,则S1:S=
(2)如图②,点P为平行四边形ABCD内任意一点时,记△PAB的面积为Sˊ,△PCD的面积为S〞,平行四边形ABCD的面积为S,猜想得Sˊ、S〞的和与S的数量关系式为
(3)如图③,已知点P为平行四边形ABCD内任意一点,△PAB的面积为3,△PBC的面积为7,求△PBD的面积.

考点:平行四边形的性质
专题:
分析:(1)由四边形ABCD是平行四边形,AD∥BC,AB∥CD,可得△BCM与?ABCD等底等高,则可求得答案;
(2)首先过点P作PE⊥AB于点E,延长EP交CD于点F,可得S′+S″=
AB•PE+
CD•PF=
AB•(PE+PF)=
AB•EF=
S;
(3)由△PAB的面积为3,△PBC的面积为7,根据(1),(2)可得:S△PBD=S四边形PBCD-S△PCD=S△PBC+S△PCD-S△BCD,继而求得答案.
(2)首先过点P作PE⊥AB于点E,延长EP交CD于点F,可得S′+S″=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由△PAB的面积为3,△PBC的面积为7,根据(1),(2)可得:S△PBD=S四边形PBCD-S△PCD=S△PBC+S△PCD-S△BCD,继而求得答案.
解答: 解:(1)∵四边形ABCD是平行四边形,AD∥BC,AB∥CD,
解:(1)∵四边形ABCD是平行四边形,AD∥BC,AB∥CD,
∴△BCM与?ABCD等底等高,
∴S1:S=1:2;
故答案为:1:2.
(2)Sˊ+S〞=
S.
理由:过点P作PE⊥AB于点E,延长EP交CD于点F,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴PF⊥CD,
∴S′+S″=
AB•PE+
CD•PF=
AB•(PE+PF)=
AB•EF=
S.
故答案为:Sˊ+S〞=
S;
(3)∵S△PAB+S△PCD=
S=S△BCD,S△PAB=3,S△PBC=7,
∴S△PBD=S四边形PBCD-S△PCD=S△PBC+S△PCD-S△BCD,
即S△PBD=7+(
S-3)-
S=7-3=4.
 解:(1)∵四边形ABCD是平行四边形,AD∥BC,AB∥CD,
解:(1)∵四边形ABCD是平行四边形,AD∥BC,AB∥CD,∴△BCM与?ABCD等底等高,
∴S1:S=1:2;
故答案为:1:2.
(2)Sˊ+S〞=
| 1 |
| 2 |
理由:过点P作PE⊥AB于点E,延长EP交CD于点F,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴PF⊥CD,
∴S′+S″=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:Sˊ+S〞=
| 1 |
| 2 |
(3)∵S△PAB+S△PCD=
| 1 |
| 2 |
∴S△PBD=S四边形PBCD-S△PCD=S△PBC+S△PCD-S△BCD,
即S△PBD=7+(
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了平行西四边形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,已知AB∥CD,∠1=∠2,你能判断AE∥DF吗?说说你的理由.
如图,已知AB∥CD,∠1=∠2,你能判断AE∥DF吗?说说你的理由. 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.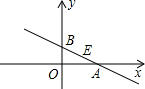 如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2,1).
如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2,1).