题目内容
 如图,已知正方形ABCD的边长是2,∠EAF=m°,将∠EAF绕点A顺时针旋转,它的两边分别交BC、CD于点E、F,G是CB延长线上一点,且始终保持BG=DF.
如图,已知正方形ABCD的边长是2,∠EAF=m°,将∠EAF绕点A顺时针旋转,它的两边分别交BC、CD于点E、F,G是CB延长线上一点,且始终保持BG=DF.(1)求证:△ABG≌△ADF;
(2)求证:AG⊥AF;
(3)当EF=BE+DF时,①求m的值;②若F是CD的中点,求BE的长.
考点:正方形的性质,全等三角形的判定与性质,勾股定理,旋转的性质
专题:
分析:(1)在正方形ABCD中,AB=AD=BC=CD=2,∠BAD=∠C=∠D=∠ABC=∠ABG=90°.已知BG=DF,所以得出△ABG≌△ADF,
(2)由△ABG≌△ADF,得出∠GAB=∠FAD,从而得到∠GAF=∠GAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,得出结论AG⊥AF;
(3)①:由△ABG≌△ADF,AG=AF,BG=DF.得到EF=BE+DF,EF=BE+BG=EG.AE=AE,得出△AEG≌△AEF.所以∠EAG=∠EAF,∠EAF=
∠GAF=45°,即m=45;
②若F是CD的中点,则DF=CF=BG=1.设BE=x,则CE=2-x,EF=EG=1+x.在Rt△CEF中,利用勾股定理得出BE的长为
.
(2)由△ABG≌△ADF,得出∠GAB=∠FAD,从而得到∠GAF=∠GAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,得出结论AG⊥AF;
(3)①:由△ABG≌△ADF,AG=AF,BG=DF.得到EF=BE+DF,EF=BE+BG=EG.AE=AE,得出△AEG≌△AEF.所以∠EAG=∠EAF,∠EAF=
| 1 |
| 2 |
②若F是CD的中点,则DF=CF=BG=1.设BE=x,则CE=2-x,EF=EG=1+x.在Rt△CEF中,利用勾股定理得出BE的长为
| 2 |
| 3 |
解答: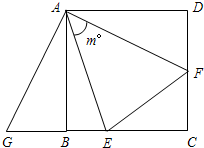
解:(1)证明:在正方形ABCD中,
AB=AD=BC=CD=2,
∠BAD=∠C=∠D=∠ABC=∠ABG=90°.
∵BG=DF,
在∴△ABG和△ADF
∴△ABG≌△ADF(SAS);
(2)证明:∵△ABG≌△ADF,
∴∠GAB=∠FAD,
∴∠GAF=∠GAB+∠BAF
=∠FAD+∠BAF=∠BAD=90°,
∴AG⊥AF;
(3)①解:△ABG≌△ADF,
∴AG=AF,BG=DF.
∵EF=BE+DF,
∴EF=BE+BG=EG.
∵AE=AE,
在△AEG和△AEF中.
∴
∴△AEG≌△AEF(SSS).
∴∠EAG=∠EAF,
∴∠EAF=
∠GAF=45°,
即m=45;
②若F是CD的中点,则DF=CF=BG=1.
设BE=x,则CE=2-x,EF=EG=1+x.
在Rt△CEF中,CE 2+CF 2=EF 2,即( 2-x ) 2+1 2=( 1+x ) 2,得x=
.
∴BE的长为
.

解:(1)证明:在正方形ABCD中,
AB=AD=BC=CD=2,
∠BAD=∠C=∠D=∠ABC=∠ABG=90°.
∵BG=DF,
在∴△ABG和△ADF
|
∴△ABG≌△ADF(SAS);
(2)证明:∵△ABG≌△ADF,
∴∠GAB=∠FAD,
∴∠GAF=∠GAB+∠BAF
=∠FAD+∠BAF=∠BAD=90°,
∴AG⊥AF;
(3)①解:△ABG≌△ADF,
∴AG=AF,BG=DF.
∵EF=BE+DF,
∴EF=BE+BG=EG.
∵AE=AE,
在△AEG和△AEF中.
∴
|
∴△AEG≌△AEF(SSS).
∴∠EAG=∠EAF,
∴∠EAF=
| 1 |
| 2 |
即m=45;
②若F是CD的中点,则DF=CF=BG=1.
设BE=x,则CE=2-x,EF=EG=1+x.
在Rt△CEF中,CE 2+CF 2=EF 2,即( 2-x ) 2+1 2=( 1+x ) 2,得x=
| 2 |
| 3 |
∴BE的长为
| 2 |
| 3 |
点评:本题主要考查了正方形的性质,全等三角形的判定与性质,勾股定理及旋转的性质,解题的关键是根据三角形全等求出相等的角与边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线y=3x-1与y=x-t的交点在第四象限,则常数t的取值范围是( )
A、t<
| ||
B、
| ||
| C、t>1 | ||
D、t>1或t<
|
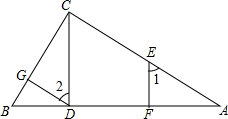 已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC
已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC 如图,已知AB∥CD,∠1=∠2,你能判断AE∥DF吗?说说你的理由.
如图,已知AB∥CD,∠1=∠2,你能判断AE∥DF吗?说说你的理由.