题目内容
5.①有一个三角形,它的内角分别为:20°,40°,120°,请你把这个三角形分成两个等腰三角形.画出你分割的示意图并标注必要的角度.②如图,在正方形ABCD所在的平面内找一点P,使其与正方形中的每一边所构成的三角形均为等腰三角形,这样的点有9个.
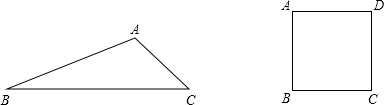
分析 ①因为∠A=120°,可以以A为顶点作∠BAP=20°,则∠PAC=100°,∠APC=40°,所以△APB,△APC都是等腰三角形;还可以以A为顶点作∠BAP=80°,则∠PAC=40°,∠APC=100°,所以△APB,△APC都是等腰三角形;
②根据正方形的性质可得,满足这样的点首先有:两条对角线的交点;再以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.根据半径相等,这些点就是要求的点.
解答 解:①如图所示:
②如图所示:9个.两条对角线的交点是一个.
以四个顶点为圆心以边长为半径画圆,在正方形里面和外面的交点一共有8个.
这些点就是要求的点.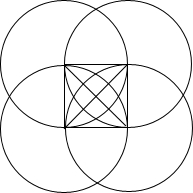
点评 本题主要考查了作图-应用与设计作图、等腰三角形的判定、正方形的性质以及作图,难度中等.确定分割三角形中的哪一个角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
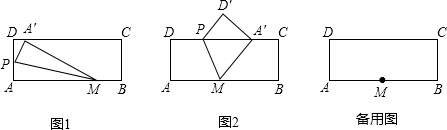
 如图,求封闭图形的面积.
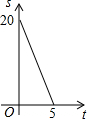
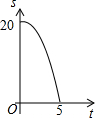
如图,求封闭图形的面积.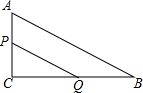 如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )
如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )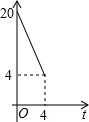
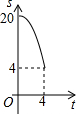
 如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,若S△AOD=4,S△BOC=9,则S梯形ABCD=25.
如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,若S△AOD=4,S△BOC=9,则S梯形ABCD=25.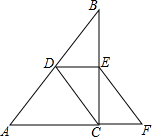 已知:如图,在△ABC中,D,E分别是AB,BC的中点,点F在AC的延长线上,且CF=DE.求证:DC∥EF.
已知:如图,在△ABC中,D,E分别是AB,BC的中点,点F在AC的延长线上,且CF=DE.求证:DC∥EF.