题目内容
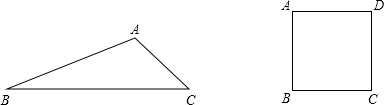
15.操作:已知矩形ABCD中,AB=5cm,AD=2cm.作如下折叠操作:如图①和图②所示,在边AB上取点M,在边AD或边DC上取点P,连结MP,将△AMP或四边形AMPD沿着直线MP折叠得到△A′MP或四边形A′MPD′,点A的落点为点A′,点D的落点为点D′.
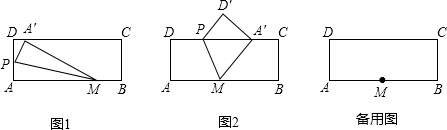
探究:(1)如图①,若AM=4cm,点P在AD上,点A′落在DC上,求∠MA′C的度数;
(2)如图②,若AM=2.5cm.
①点P在DC上,点A′落在DC上,求线段DP的长;
②若点P由A开始,沿A→D→C方向,在AD、DC边上运动.设点P的运动速度为1cm/s,运动时间为ts,当边MA′与线段DC有交点时,直接写出t的取值范围1.25≤t≤3.5.
发现:
(3)若点M在线段AB上移动,点P为线段AD或DC边上的任意点,随着点M位置的不同,按操作要求折叠后,点A的落点A′的位置会出现以下三种不同的情况:①不会落在线段DC上;②只有一次落在线段DC上;③会有两次落在线段DC上.
求:在②③的情况下,AM的取值范围.
分析 (1)根据折叠的性质得出三角形全等,进而分析AM=A′M=8=2MN,利用含30°角的直角三角形的性质解答即可;
(2)①根据矩形的性质和翻折的性质得出∠A′PM=∠A′MP,再利用等角对等边得出等腰三角形,根据等腰三角形中边之间的关系得出线段的长度即可;
②根据勾股定理得出t的取值范围;
(3)利用矩形的性质作图进行解答.
解答 解:(1)过点M作MN⊥DC,如图1: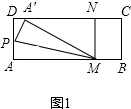
∵四边形ABCD是矩形,
∴MN=BC=2,
∵将△AMP沿着直线MP折叠得到△A′MP,
∴AM=A′M=4=2MN,
∴在Rt△A′MN中,∠MA′C=30°;
(2)①∵A′P与AM是矩形ABCD的对边CD,AB的一部分,
∴A′P∥AM,
∴∠A′PM=∠AMP,
由翻折的性质得:∠AMP=∠A′MP,
∴∠A′PM=∠A′MP,
∴A′P=A′M,
∴△MA′P是等腰三角形;
∴PM=AM=A′M=2.5,
∵DA=2,
∴DP=2.5-2=0.5
∴线段DP的长是0.5cm;
②当点P在AD上,点A′落在DC上时,如图1所示,
过点M作MN⊥DC交DC于点N,
则四边形AMND为矩形,DN=AM=2.5cm,MN=2cm,
设AP为xcm,则由翻折的性质得:
AM=A′M=2.5cm,AP=A′P=xcm,
在Rt△A′MN中,A′N=$\sqrt{2.{5}^{2}-{2}^{2}}=1.5$cm,
∴DA′=DN-A′N=2.5-1.5=1(cm),
在Rt△A′PD中,
A′P2=A′D2+PD2,
即:x2=12+(2-x)2,
解得:x=1.25,
此时t=1.25s;
当点P在DC上,点A′落在DC上时,如图1,
可知DP=1.5cm,此时,t=3.5s,
当MA′与DC有交点时,t的取值范围是:1.25≤t≤3.5;
故答案为:1.25≤t≤3.5;
(3)当点A′到边AB的距离最大时,
即A′M⊥AB时,t的值为2.5s,
发现:当点A的落点A′,在以M为圆心,MA为半径的圆上,当圆M与线段CD有唯一交点时,如图2所示,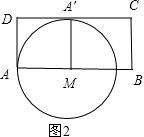
此时AM=2cm,
当圆M交线段CD于点C时,如图3所示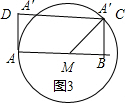
AM=2.9cm,
所以:2<AM≤2.9.
点评 此题考查几何变换问题,用到的知识点是等腰三角形的判定与性质、矩形的性质、勾股定理,关键是利用折叠的前后图形全等进行分析,同时利用矩形的性质和等腰三角形的判定和性质进行解答.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
| A. | a-b<0 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -a>-b | D. | -a+1<-b+1 |
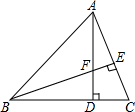 如图,AD,BE为△ABC的高,交点为F,且有BF=AC,FD=CD,证明:BD=AD.
如图,AD,BE为△ABC的高,交点为F,且有BF=AC,FD=CD,证明:BD=AD. 小球在如图所示的地板上自由地滚动,并随机地停留在某块方砖上,那么小球最终停留在黑色区域的概率是$\frac{2}{9}$.
小球在如图所示的地板上自由地滚动,并随机地停留在某块方砖上,那么小球最终停留在黑色区域的概率是$\frac{2}{9}$. 如图,点A(m,2),B(5,n)在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,将该函数图象向上平移2个单位长度得到一条新的曲线,点A、B的对应点分别为A′、B′.图中阴影部分的面积为8,则k的值为2.
如图,点A(m,2),B(5,n)在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,将该函数图象向上平移2个单位长度得到一条新的曲线,点A、B的对应点分别为A′、B′.图中阴影部分的面积为8,则k的值为2.