题目内容
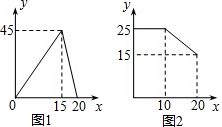
15.如图,某水果店购进一批时令水果,在20天内销售完毕.店主将本次销售数据绘制成函数图象.如图1,日销售量y(千克)与销售时间x(天)之间的函数关系;如图2,销售单价p(元/千克)与销售时间x(天)之间的函数关系.(1)求y关于x和p关于x的函数关系式;
(2)若日销售量不低于36千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售金额最高是第几天?
分析 (1)分两种情况进行讨论:①0≤x≤15;②15<x≤20;针对每一种情况,都可以先设出函数的解析式,再将已知点的坐标代入,利用待定系数法求解;
(2)日销售金额=日销售单价×日销售量.由于第10天和第15天在第10天和第20天之间,当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数关系式为p=mx+n,由点(10,25),(20,15)在p=mx+n的图象上,利用待定系数法求得p与x的函数解析式,日销售量不低于36千克,即y≥36.先解不等式2x≥36,得x≥13,再解不等式-9x+180≥36,得x≤16,则求出“最佳销售期”共有4天;然后根据p=-x+35(10≤x≤20),利用一次函数的性质,即可解答.
解答 解:(1)分两种情况:
①当0≤x≤15时,设日销售量y与销售时间x的函数解析式为y=k1x,
∵直线y=k1x过点(15,45),
∴15k1=45,解得k1=3,
∴y=3x(0≤x≤15);
②当15<x≤20时,设日销售量y与销售时间x的函数解析式为y=k2x+b,
∵点(15,45),(20,0)在y=k2x+b的图象上,
∴$\left\{\begin{array}{l}{15{k}_{2}+b=45}\\{20{k}_{2}+b=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{2}=-9}\\{b=180}\end{array}\right.$
∴y=-9x+180(15<x≤20);
综上,可知y与x之间的函数关系式为:y=$\left\{\begin{array}{l}{3x(0≤x≤15)}\\{-9x+180(15<x≤20)}\end{array}\right.$.
(2)∵第10天和第15天在第10天和第20天之间,
∴当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数解析式为p=mx+n,
∵点(10,25),(20,15)在p=mx+n的图象上,
∴$\left\{\begin{array}{l}{10m+n=25}\\{20m+n=15}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=-1}\\{n=35}\end{array}\right.$
∴y=-x+35(10≤x≤20),
若日销售量不低于36千克,则y≥36.
当0≤x≤15时,y=2x,
解不等式:2x≥36,
得,x≥13;
当15<x≤20时,y=-9x+180,
解不等式:-9x+180≥36,
得x≤16,
∴13≤x≤16,
∴“最佳销售期”共有:16-13+1=4(天);
∵p=-x+35(10≤x≤20),k=-1<0,
∴p随x的增大而减小,
∴当13≤x≤16时,x取13时,p有最大值,此时p=-13+35=22(元/千克).
答:此次销售过程中“最佳销售期”共有4天,在此期间销售金额最高是第13天.
点评 此题考查了一次函数的应用,有一定难度.解题的关键是理解题意,利用待定系数法求得函数解析式,注意数形结合思想与函数思想的应用.

 阅读快车系列答案
阅读快车系列答案| A. | 明天某地区早晨有雾 | |
| B. | 抛掷一枚质地均匀的骰子,向上一面的点数是6 | |
| C. | 一个不透明的袋子中有2个红球和1个白球,从中摸出1个球,该球是黑球 | |
| D. | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
 已知:如图,在△ABC中,∠ABC、∠ACB的平分线相交于I,求证:∠BIC=90°+$\frac{1}{2}$∠A.
已知:如图,在△ABC中,∠ABC、∠ACB的平分线相交于I,求证:∠BIC=90°+$\frac{1}{2}$∠A.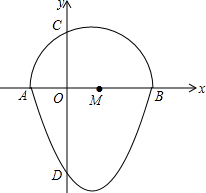 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(-2,0),B点坐标为(4,0),D点的坐标为(0,-4).
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(-2,0),B点坐标为(4,0),D点的坐标为(0,-4).