题目内容
17．
如图，在梯形ABCD中，AD∥BC，AC与BD交于点O，若S△AOD=4，S△BOC=9，则S梯形ABCD=25．
分析 由梯形ABCD中AD∥BC，可得△AOD∽△COB，然后由相似三角形面积比等于相似比的平方，求得△BOC的面积，又由等高三角形的面积的比等于对应底的比，可求得△AOB与△COD的面积，继而求得答案．
解答 解：∵梯形ABCD中AD∥BC，
∴△AOD∽△COB，
∴S△AOD：S△BOC=4：9，
∴OA：OC=AD：BC=2：3，
∵S△AOD=4，S△BOC=9，
∴S△AOB=S△COD=$\frac{3}{2}$S△AOD=6，
∴梯形ABCD的面积为：S△AOD+S△AOB+S△BOC+S△COD=25．
故答案为：25．
点评 此题考查了梯形的性质以及相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
同步练习强化拓展系列答案
相关题目
小球在如图所示的地板上自由地滚动，并随机地停留在某块方砖上，那么小球最终停留在黑色区域的概率是$\frac{2}{9}$．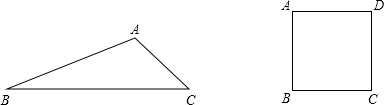
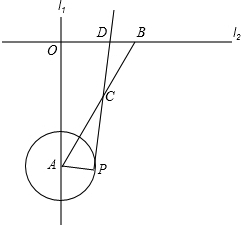如图，直线l1⊥l2，垂足为O，点A、B分别在直线l1和l2上，∠OAB=30°，OB=2，以A为圆心，1为半径画圆，点P在圆A的圆周上运动，连接AP，过点P画PA的垂线与线段AB相交于点C，与直线l2相交于D，当AC=BC时，OD的长是1或4．
如图，已知BE是△ABC的外接圆的直径，CD⊥AB于D，若AD=3，BD=8，CD=6，则BE的长为5$\sqrt{5}$．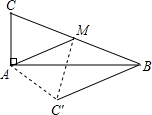
如图，在Rt△ABC中，∠BAC=90°，点M为斜边BC的中点，AM=5厘米，∠AMC=45°，将△AMC沿AM翻折，点C落在△ABC所在平面内的C′处，那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米．
6．下列事件中，属于不可能事件的是（ ）
| A． | 明天某地区早晨有雾 | |
| B． | 抛掷一枚质地均匀的骰子，向上一面的点数是6 | |
| C． | 一个不透明的袋子中有2个红球和1个白球，从中摸出1个球，该球是黑球 | |
| D． | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
