题目内容
15.若三角形的某一边长等于其外接圆半径,则将此三角形称为等径三角形,该边所对的角称为等径角.已知△ABC是等径三角形,则等径角的度数为30°或150°.分析 根据边长等于半径时,边长所对的圆心角为60°,根据圆周角与圆心角的关系和圆内接四边形的性质求出等径角的度数.
解答 解:如图边AB与半径相等时,
则∠AOB=60°,
当等径角顶点为C时,∠C=$\frac{1}{2}$∠AOB=30°,
当等径角顶点为D时,∠C+∠D=180°,∠D=150°,
故答案为:30°或150°.
点评 本题考查的是三角形的外接圆的知识,掌握圆周角与圆心角的关系和圆内接四边形的性质是解题的关键,根据等边三角形的性质求出圆心角是重点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在锐角△ABC中,|sinA-$\frac{\sqrt{3}}{2}$|+(cosB-$\frac{\sqrt{2}}{2}$)2=0,则∠C的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
7.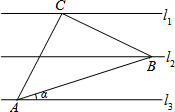 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{6}{17}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
4.多项式x2-x-12可以因式分解成( )
| A. | (x+3)(x+4) | B. | (x-3)(x+4) | C. | (x+3)(x-4) | D. | (x-3)(x-4) |
5.已知三角形三边长分别为12,13,5,则这个三角形的面积为( )
| A. | 78 | B. | 65 | C. | 60 | D. | 30 |
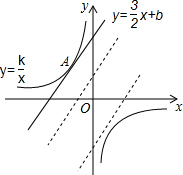 如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.
如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.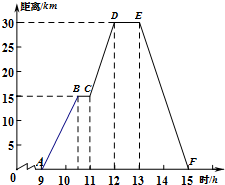 小强骑自行车去郊游,9时出发,15时返回.右图表示他距家的距离y(千米)与相应的时刻x(时)之间的函数关系的图象.根据这个图象,小强14时距家的距离是( )
小强骑自行车去郊游,9时出发,15时返回.右图表示他距家的距离y(千米)与相应的时刻x(时)之间的函数关系的图象.根据这个图象,小强14时距家的距离是( )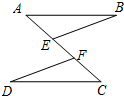 如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.
如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.