题目内容
6．在锐角△ABC中，|sinA-$\frac{\sqrt{3}}{2}$|+（cosB-$\frac{\sqrt{2}}{2}$）2=0，则∠C的度数是（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
分析 根据非负数的性质求出∠A和∠B的度数，然后求出∠C的度数．
解答 解：由题意得，sinA-$\frac{\sqrt{3}}{2}$=0，cosB-$\frac{\sqrt{2}}{2}$=0，
则sinA=$\frac{\sqrt{3}}{2}$，cosB=$\frac{\sqrt{2}}{2}$，
∠A=45°，∠B=45°，
则∠C=180°-45°-45°=90°．
故选D．
点评 本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．
练习册系列答案
相关题目
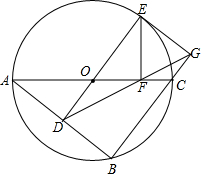如图，⊙O是△ABC的外接圆，AC是直径，过O作OD∥BC交AB于点D．延长DO交⊙O于点E，作EF⊥AC于点F．连接DF并延长交直线BC于点G，连接EG．
如图，⊙M和⊙N都与x轴和y轴相切，圆心A与圆心B都在反比例函数y=$\frac{-1}{x}$的图象上，则图中阴影部分面积等于π．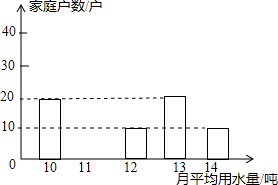
为了倡导“节约用水，从我做起”，某市政府决定对市直机关500户家庭的用水情况作一次调查．市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量（单位：吨），并将调查结果制成了如图所示的条形统计图．
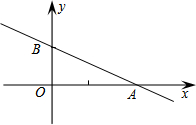如图，在以点O为原点的直角坐标系中，一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A，与y轴交于点B，点C在第二象限内且为直线AB上一点，OC=$\frac{1}{2}$AB，反比例函数y=$\frac{k}{x}$的图象经过点C，则k的值为-$\frac{11}{50}$．
16．下列各式能用完全平方式进行分解因式的是（ ）
| A． | x2+1 | B． | x2+2x-1 | C． | x2+x+1 | D． | ${x^2}-x+\frac{1}{4}$ |