题目内容
5．已知三角形三边长分别为12，13，5，则这个三角形的面积为（ ）| A． | 78 | B． | 65 | C． | 60 | D． | 30 |
分析 先根据勾股定理的逆定理判定三角形是直角三角形，再利用面积公式求得面积．
解答 解：∵52+122=132，
∴三边长分别为5、12、13的三角形构成直角三角形，其中的直角边是5、12，
∴此三角形的面积为$\frac{1}{2}$×5×12=30．
故选D．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
备战中考寒假系列答案
相关题目
16．下列各式能用完全平方式进行分解因式的是（ ）
| A． | x2+1 | B． | x2+2x-1 | C． | x2+x+1 | D． | ${x^2}-x+\frac{1}{4}$ |
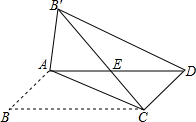如图，在?ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连接B′C，B′D，B′C交AD于点E．
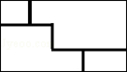夏季荷花盛开，为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的长方形荷塘上架设小桥．若荷塘周长为250m，且桥宽忽略不计，则小桥总长为125 m．