题目内容
16.$\frac{x-4}{x-2}$÷($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$),其中x满足x2=2x-2017.分析 先根据分式混合运算的法则把原式进行化简,再根据x2=2x-2017得出x2-2x=-2017,代入原式进行计算即可.
解答 解:原式=$\frac{x-4}{x-2}$÷[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]
=$\frac{x-4}{x-2}$÷$\frac{(x+2)(x-2)-x(x-1)}{x(x-2)^{2}}$
=$\frac{x-4}{x-2}$÷$\frac{x-4}{x(x-2)^{2}}$
=$\frac{x-4}{x-2}$•$\frac{x(x-2)^{2}}{x-4}$
=x(x-2)
=x2-2x,
∵x2=2x-2017,
∴x2-2x=-2017,
∴原式=-2017.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
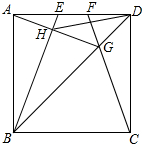 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )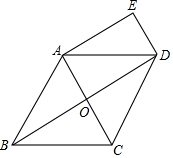 如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD. 如图,已知∠EFG+∠BDG=180°,∠DEF=∠B,求证:∠AED=∠C.
如图,已知∠EFG+∠BDG=180°,∠DEF=∠B,求证:∠AED=∠C. 如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF=64°.
如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF=64°.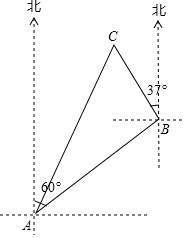 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)
一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)