题目内容
8. 如图,已知∠EFG+∠BDG=180°,∠DEF=∠B,求证:∠AED=∠C.
如图,已知∠EFG+∠BDG=180°,∠DEF=∠B,求证:∠AED=∠C.
分析 先根据平角的定义得出∠EFD+∠EFG=180°,再由同角的补角相等及内错角相等,两直线平行可判断出BD∥EF,再根据两直线平行,同旁内角互补可得到∠BDE+∠DEF=180°,进而可判断出DE∥BC,由平行线的性质即可得出答案.
解答  证明:∵∠EFD+∠EFG=180°,
证明:∵∠EFD+∠EFG=180°,
∠BDG+∠EFG=180°,
∴∠BDG=∠EFD,
∴BD∥EF,
∴∠BDE+∠DEF=180°,
又∵∠DEF=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC,
∴∠AED=∠C.
点评 本题主要考查了平行线的判定与性质,熟知平行线的判定与性质的区别是解答此题的关键,即性质与判定的已知和结论正好相反,都是角的关系与平行线相关.

练习册系列答案
相关题目
18.把分式$\frac{x+y}{xy}$中的x、y都扩大到原来的2倍,则分式的值( )
| A. | 扩大到原来的2倍 | B. | 扩大到原来的4倍 | C. | 缩小到原来的$\frac{1}{2}$ | D. | 不变 |
17. 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )| A. | DE是△ABE的高 | B. | DE是△BCD的高 | C. | AC是△ABC的高 | D. | AD是△ACD的高 |
 如果直线l1∥l2,则∠α=120°.
如果直线l1∥l2,则∠α=120°.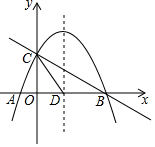 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为(2,1).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为(2,1).