题目内容
6.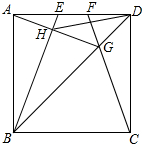 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2$\sqrt{5}$-2.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 首先证明△ABE≌△DCF,△ADG≌△CDG(SAS),△AGB≌△CGB,利用全等三角形的性质,等高模型、三边关系一一判断即可.
解答 解:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAD=∠ADC}\\{AE=DF}\end{array}\right.$,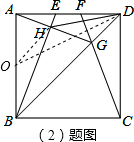
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADB=∠CDB}\\{DG=DG}\end{array}\right.$,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠ABE=∠DAG,
∵∠DAG+∠BAH=90°,
∴∠BAE+∠BAH=90°,
∴∠AHB=90°,
∴AG⊥BE,故③正确,
同法可证:△AGB≌△CGB,
∵DF∥CB,
∴△CBG∽△FDG,
∴△ABG∽△FDG,故①正确,
∵S△HDG:S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD,
又∵∠DAG=∠FCD,
∴S△HDG:S△HBG=tan∠FCD,tan∠DAG,故④正确
取AB的中点O,连接OD、OH,
∵正方形的边长为4,
∴AO=OH=$\frac{1}{2}$×4=2,
由勾股定理得,OD=$\sqrt{{4}^{2}+{2}^{2}}$=2 $\sqrt{5}$,
由三角形的三边关系得,O、D、H三点共线时,DH最小,
DH最小=2 $\sqrt{5}$-2.
无法证明DH平分∠EHG,故②错误,
故①③④⑤正确,
故选C.
点评 本题考查了正方形的性质,全等三角形的判定与性质,三角形的三边关系,勾股定理、等高模型等知识,解题的关键是灵活运用所学知识解决问题,难点在于⑤作辅助线并确定出DH最小时的情况.

| A. | 扩大到原来的2倍 | B. | 扩大到原来的4倍 | C. | 缩小到原来的$\frac{1}{2}$ | D. | 不变 |
| A. | 0是有理数 | B. | 0不是正数 | C. | 0没有相反数 | D. | 0的绝对值是0 |
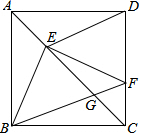 如图,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于点G,则$\frac{EG}{CG}$=$\sqrt{2}$.
如图,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于点G,则$\frac{EG}{CG}$=$\sqrt{2}$.
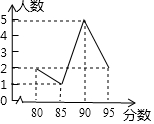 在一次“班班有诗词”竞赛活动中,某班10名学生的成绩折线统计图如图所示,若随机从这10名学生中抽取一人,则抽中概率最大的学生得分是90分.
在一次“班班有诗词”竞赛活动中,某班10名学生的成绩折线统计图如图所示,若随机从这10名学生中抽取一人,则抽中概率最大的学生得分是90分.