题目内容
5.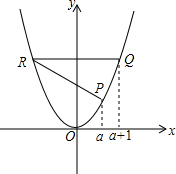 已知P,Q,R是抛物线y=x2上不同的三点,设P,Q的横坐标分别为a,a+1(a>0),R与Q是关于y轴对称的两点.
已知P,Q,R是抛物线y=x2上不同的三点,设P,Q的横坐标分别为a,a+1(a>0),R与Q是关于y轴对称的两点.(1)求△PQR的面积S关于a的关系式;
(2)当△PQR的面积S等于28时,求a的值.
分析 (1)由对称性得出RQ=2(a+1),再把P,Q的横坐标分别代入抛物线y=x2求得纵坐标,算出差,即是△PQR的高,利用三角形的面积求得关系式即可;
(2)利用(1)中的关系式建立方程求得a即可.
解答 解:(1)∵R与Q是关于y轴对称的两点,
∴RQ=2(a+1),
把点P,Q的横坐标分别代入抛物线y=x2中,
得到点P(a,a2),点Q(a+1,(a+1)2),
(a+1)2-a2=2a+1,
∴S=$\frac{1}{2}$×2(a+1)(2a+1)=2a2+3a+1;
(2)由题意得2a2+3a+1=28,
解得:a=3或a=-$\frac{9}{2}$(舍去)
答:a的值是3.
点评 此题考查二次函数的性质,三角形的面积,一元二次方程的实际运用,利用二次函数的对称性求得三角形的底是解决问题的前提.

练习册系列答案
相关题目
16.下列各式计算正确的是( )
| A. | $\sqrt{{2}^{2}+{3}^{2}}$=2+3 | B. | 3$\sqrt{2}$+5$\sqrt{3}$=8$\sqrt{6}$ | ||
| C. | $\sqrt{1{5}^{2}-1{2}^{2}}$=$\sqrt{15+12}$×$\sqrt{15-12}$ | D. | $\sqrt{4\frac{1}{2}}$=2$\sqrt{\frac{1}{2}}$ |
17.$\frac{1-2+3-4+…+19-20}{-2+4-6+8-…-38+40}$等于( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |

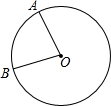 如图.点A、B把⊙O分成2:7两条弧,则∠AOB=80°.
如图.点A、B把⊙O分成2:7两条弧,则∠AOB=80°.