题目内容
17．$\frac{1-2+3-4+…+19-20}{-2+4-6+8-…-38+40}$等于（ ）| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
分析 原式分子分母结合后相加，约分即可得到结果．
解答 解：原式=$\frac{（1-2）+（3-4）+…+（19-20）}{（-2+4）+（-6+8）+…+（-38+40）}$=$\frac{-10}{20}$=-$\frac{1}{2}$，
故选D．
点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
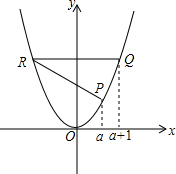已知P，Q，R是抛物线y=x2上不同的三点，设P，Q的横坐标分别为a，a+1（a＞0），R与Q是关于y轴对称的两点．
2．化简：a$\sqrt{-\frac{1}{a}}$的结果是（ ）
| A． | $\sqrt{-a}$ | B． | $\sqrt{a}$ | C． | -$\sqrt{-a}$ | D． | -$\sqrt{a}$ |
如图，在△ABC中，BC边上的高为AD，AC边上的高为BE，BC=8，AD=5，AC=6，求BE的长．