题目内容
15.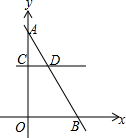 如图,直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,平行于x轴的直线CD与y轴、线段AB分别交于点C、D.若$\frac{AD}{DB}$=$\frac{1}{2}$,则点C的坐标为( )
如图,直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,平行于x轴的直线CD与y轴、线段AB分别交于点C、D.若$\frac{AD}{DB}$=$\frac{1}{2}$,则点C的坐标为( )| A. | (0,2) | B. | (0,3) | C. | (0,4) | D. | (0,6) |
分析 先求出点A的坐标,再由CD∥x轴,$\frac{AD}{DB}$=$\frac{1}{2}$可得出$\frac{AC}{OC}$的值,进而可得出结论.
解答 解:∵直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,
∴当x=0时,y=6,
∴A(0,6).
∵CD∥x轴,$\frac{AD}{DB}$=$\frac{1}{2}$,
∴$\frac{AC}{OC}$=$\frac{1}{2}$,即OC=$\frac{2}{3}$OA=$\frac{2}{3}$×6=4,
∴C(0,4).
故选C.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.若一次函数y=kx+b的图象经过(-1,1),(0,m),(1,-5)三点,则m的值为( )
| A. | -1 | B. | -2 | C. | 0 | D. | $\frac{1}{2}$ |
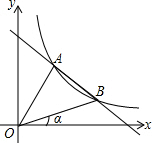 如图,直线y=kx+b(k≠0),与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一象限内的A、B两点,已知点A的坐标为(3,4),OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.
如图,直线y=kx+b(k≠0),与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一象限内的A、B两点,已知点A的坐标为(3,4),OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$. 如图,AC是矩形ABCD的对角线,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,然后再在图中画出矩形ABCD的外接圆.(用尺规作图,写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
如图,AC是矩形ABCD的对角线,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,然后再在图中画出矩形ABCD的外接圆.(用尺规作图,写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).