题目内容
3.若一次函数y=kx+b的图象经过(-1,1),(0,m),(1,-5)三点,则m的值为( )| A. | -1 | B. | -2 | C. | 0 | D. | $\frac{1}{2}$ |
分析 先利用待定系数法求出一次函数y=kx+b的解析式,再把(0,m)代入求出m的值即可.
解答 解:∵点(-1,1),(1,-5)在一次函数y=kx+b的图象上,
∴$\left\{\begin{array}{l}1=-k+b\\-5=k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=-3\\ b=-2\end{array}\right.$,
∴一次函数的解析式为y=-3x-2.
∵点(0,m)在此函数图象上,
∴m=-2.
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
15.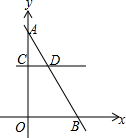 如图,直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,平行于x轴的直线CD与y轴、线段AB分别交于点C、D.若$\frac{AD}{DB}$=$\frac{1}{2}$,则点C的坐标为( )
如图,直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,平行于x轴的直线CD与y轴、线段AB分别交于点C、D.若$\frac{AD}{DB}$=$\frac{1}{2}$,则点C的坐标为( )
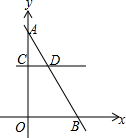 如图,直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,平行于x轴的直线CD与y轴、线段AB分别交于点C、D.若$\frac{AD}{DB}$=$\frac{1}{2}$,则点C的坐标为( )
如图,直线y=kx+6(k<0)与y轴、x轴分别交于点A、B,平行于x轴的直线CD与y轴、线段AB分别交于点C、D.若$\frac{AD}{DB}$=$\frac{1}{2}$,则点C的坐标为( )| A. | (0,2) | B. | (0,3) | C. | (0,4) | D. | (0,6) |
 南宁市在中国水城建设中,某施工队为引水需要欲拆除琶江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道.($\sqrt{3}$≈1.73).
南宁市在中国水城建设中,某施工队为引水需要欲拆除琶江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道.($\sqrt{3}$≈1.73).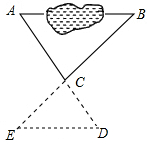 如图,A、B两点被池塘隔开,小吴为了测量A,B两点间的距离,他在AB外选一点C,连接AC和BC,延长AC到D,使CD=$\frac{1}{2}$AC,延长BC到E,使CE=$\frac{1}{2}$BC,连接DE.若小吴测得DE的长为400米,根据以上信息,请你求出AB的长.
如图,A、B两点被池塘隔开,小吴为了测量A,B两点间的距离,他在AB外选一点C,连接AC和BC,延长AC到D,使CD=$\frac{1}{2}$AC,延长BC到E,使CE=$\frac{1}{2}$BC,连接DE.若小吴测得DE的长为400米,根据以上信息,请你求出AB的长.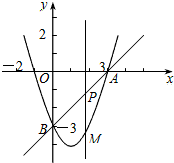 如图,在平面直角坐标系中,抛物线y=x2-2x-3和直线y=x-3经过点A、B,点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
如图,在平面直角坐标系中,抛物线y=x2-2x-3和直线y=x-3经过点A、B,点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.