��Ŀ����
10�����������а���Ķ�Ͳ˻���ÿ�괺�죬ʢ�����Ͳ˻�����ɽ��ˮ���ӳ������һ�������ķ羰����Ӱ������С�ɺ�СЦ�ƻ����Ͳ˻��ڽ������㣬���������Ͳ˻����ֲ���Χ�㷺������С�ɺ�СЦ�������ó�ǩ�ķ�ʽ��1-��֣��2-���磬3-��̨��4-���أ�5-����������ط���ѡ�������ط��������㣬��ǩ�������£�������ص�ֱ�д�����ű�����ͬ�Ŀ�Ƭ�ϣ�С���������ȡһ�ſ�Ƭ�����Żأ����Ⱥ�СЦ�ٳ�ȡһ�ţ���1��С�ɳ�ȡ���ĵص�����֣�ĸ����Ƕ��٣�
��2��������״ͼ���б��ķ�������С�ɺ�СЦ�����غͺ�̨�������ط���������ĸ��ʣ�
���� ��1���ɹ�����ط���1-��֣��2-���磬3-��̨��4-���أ�5-���أ�ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����С�ɺ�СЦ�����غͺ�̨�������ط��������������������ø��ʹ�ʽ������ô𰸣�
��� �⣺��1���߹�����ط���1-��֣��2-���磬3-��̨��4-���أ�5-���أ�
��С�ɳ�ȡ���ĵص�����֣�ĸ����ǣ�$\frac{1}{5}$��
��2������״ͼ�ã�
�߹���20�ֵȿ��ܵĽ����С�ɺ�СЦ�����غͺ�̨�������ط������������2�������
��С�ɺ�СЦ�����غͺ�̨�������ط���������ĸ���Ϊ��$\frac{2}{20}$=$\frac{1}{10}$��
���� ���⿼�����б�������״ͼ������ʣ��õ���֪ʶ��Ϊ������=������������������֮�ȣ�

��ϰ��ϵ�д�
 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
�����Ŀ
1��������x�ķ���x2-4x+m+4=0��ʵ��������m��ȡֵ��Χ�ǣ�������
| A�� | m��0 | B�� | m��0 | C�� | m��0 | D�� | m��0 |
15��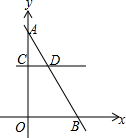 ��ͼ��ֱ��y=kx+6��k��0����y�ᡢx��ֱ��ڵ�A��B��ƽ����x���ֱ��CD��y�ᡢ�߶�AB�ֱ��ڵ�C��D����$\frac{AD}{DB}$=$\frac{1}{2}$�����C������Ϊ��������
��ͼ��ֱ��y=kx+6��k��0����y�ᡢx��ֱ��ڵ�A��B��ƽ����x���ֱ��CD��y�ᡢ�߶�AB�ֱ��ڵ�C��D����$\frac{AD}{DB}$=$\frac{1}{2}$�����C������Ϊ��������
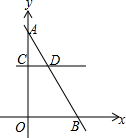 ��ͼ��ֱ��y=kx+6��k��0����y�ᡢx��ֱ��ڵ�A��B��ƽ����x���ֱ��CD��y�ᡢ�߶�AB�ֱ��ڵ�C��D����$\frac{AD}{DB}$=$\frac{1}{2}$�����C������Ϊ��������
��ͼ��ֱ��y=kx+6��k��0����y�ᡢx��ֱ��ڵ�A��B��ƽ����x���ֱ��CD��y�ᡢ�߶�AB�ֱ��ڵ�C��D����$\frac{AD}{DB}$=$\frac{1}{2}$�����C������Ϊ��������| A�� | ��0��2�� | B�� | ��0��3�� | C�� | ��0��4�� | D�� | ��0��6�� |
19�����������У���ȷ���ǣ�������
| A�� | m2•m3=m6 | B�� | ��-m2��3=m6 | C�� | -m2-2m2=-3m2 | D�� | -3m-2=-$\frac{1}{9{m}^{2}}$ |
20��ijͬѧ�����б���㷨�����κ���y=ax2+bx+c��ͼ��ʱ���г�������ı�����ô��x=5ʱ��y��ֵΪ��������
| ��x | �� | -1�� | 0 | 1�� | 2 | 3�� | �� |
| y | �� | 8 | 3�� | 0 | -1 | 0 | �� |
| A�� | 8 | B�� | 6 | C�� | 4 | D�� | 3 |
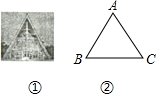 ��ͼ��ij��A�����ͼ�������ͼ����ʾ�����������ƽ��ͼ��ͼ����ʾ����á�B=��C=62�㣬BC=10.22�ף����ݶ�A������BC�ľ��루�����ȷ��0.1�ף�
��ͼ��ij��A�����ͼ�������ͼ����ʾ�����������ƽ��ͼ��ͼ����ʾ����á�B=��C=62�㣬BC=10.22�ף����ݶ�A������BC�ľ��루�����ȷ��0.1�ף�