题目内容
函数y=-x2的对称轴是 ,顶点坐标是 ,图象开口向 ,当x 时,y随x的增大而减小,当x 时,函数y有最 值,是 .
考点:二次函数的性质
专题:
分析:根据二次函数的对称轴,顶点坐标,图象开口方向,二次函数的增减性填空即可.
解答:解:函数y=-x2的对称轴是y轴,顶点坐标是(0,0),图象开口向下,
当x>0时,y随x的增大而减小,当x=0时,函数y有最大值,是0.
故答案为:y轴;(0,0);下;>0;=0;大;0.
当x>0时,y随x的增大而减小,当x=0时,函数y有最大值,是0.
故答案为:y轴;(0,0);下;>0;=0;大;0.
点评:本题考查了二次函数的性质,是基础题,熟记性质是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
下列说法错误的是( )
| A、有一个角等于60°的两个等腰三角形相似 |
| B、有一个角等于100°的两个等腰三角形相似 |
| C、有一个角等于90°的两个等腰三角形相似 |
| D、有一个角等于30°的两个等腰三角形相似 |
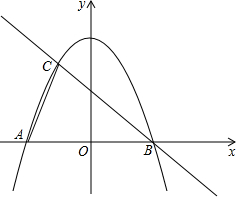 如图,抛物线y=
如图,抛物线y= 如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,已知⊙O的半径为5cm,AE=3cm,BF=5cm,求CD的长.
如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,已知⊙O的半径为5cm,AE=3cm,BF=5cm,求CD的长.