题目内容
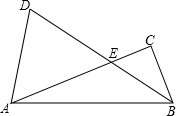 在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当
在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当| AD |
| BE |
| 3 |
考点:旋转的性质
专题:计算题
分析:作BF⊥AD于F,如图,由旋转的性质得BA=BD,∠ABD=2α,则根据等腰三角形的性质得到BF⊥AD,BF平分∠ABD,AF=DF,再利用“AAS”证明△ABC≌△ABF,得到AF=BC,由于
=
,则AF=
BE=BC,在Rt△BCE中,根据正弦的定义可计算出∠CEB=60°,然后根据三角形外角性质得∠CEB=α+2α=60°,易得α=20°.
| AD |
| BE |
| 3 |
| ||
| 2 |
解答:解:作BF⊥AD于F,如图,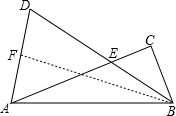
∵边AB绕点B按顺时针方向旋转2α得到DB,
∴BA=BD,∠ABD=2α,
∴BF⊥AD,BF平分∠ABD,AF=DF,
∴∠ABF=α,
在△ABC和△ABF中,
,
∴△ABC≌△ABF(AAS),
∴AF=BC,
∵
=
,
∴AF=
BE,
∴BC=
BE,
在Rt△BCE中,∵sin∠CEB=
=
,
∴∠CEB=60°,
∴∠CEB=∠EAB+∠EBA=α+2α,
即α+2α=60°,
∴α=20°.
故答案为20°.

∵边AB绕点B按顺时针方向旋转2α得到DB,
∴BA=BD,∠ABD=2α,
∴BF⊥AD,BF平分∠ABD,AF=DF,
∴∠ABF=α,
在△ABC和△ABF中,
|
∴△ABC≌△ABF(AAS),
∴AF=BC,
∵
| AD |
| BE |
| 3 |
∴AF=
| ||
| 2 |
∴BC=
| ||
| 2 |
在Rt△BCE中,∵sin∠CEB=
| BC |
| BE |
| ||
| 2 |
∴∠CEB=60°,
∴∠CEB=∠EAB+∠EBA=α+2α,
即α+2α=60°,
∴α=20°.
故答案为20°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和锐角三角函数.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、两腰对应相等的两个等腰三角形全等 |
| B、两角及其夹边对应相等的两个三角形全等 |
| C、两锐角对应相等的两个直角三角形全等 |
| D、面积相等的两个三角形全等 |
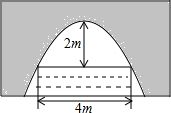 有一座抛物线形拱桥,正常水位时桥下水面宽度为4m,拱顶距离水面 2m.
有一座抛物线形拱桥,正常水位时桥下水面宽度为4m,拱顶距离水面 2m.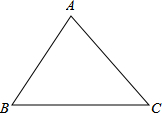 从三角形木板上截下一块圆形的木板,
从三角形木板上截下一块圆形的木板,