题目内容
3.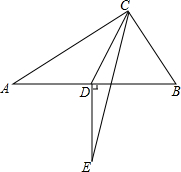 已知,如图:在△ABC中,∠ACB=90°,AB的垂直平分线DE,交∠ACB的平分线于点E,交AB于点D.
已知,如图:在△ABC中,∠ACB=90°,AB的垂直平分线DE,交∠ACB的平分线于点E,交AB于点D.求证:CD=ED.
分析 过E作EM⊥AC于M,EN⊥BC于N,连接AE、BE,根据垂直平分线的性质和角平分线的性质得出AE=BE,EM=EN,∠AME=∠N=90°,证Rt△AME≌Rt△BNE,推出∠AEM=∠BEN,求出∠AEB=90°,根据直角三角形性质得出ED=$\frac{1}{2}$AB,CD=$\frac{1}{2}$AB,即可得出答案.
解答 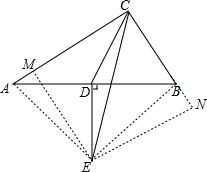 证明:过E作EM⊥AC于M,EN⊥BC于N,连接AE、BE,
证明:过E作EM⊥AC于M,EN⊥BC于N,连接AE、BE,
∵DE为AB的垂直平分线,CE是∠ACB的角平分线,
∴AE=BE,EM=EN,∠AME=∠N=90°,
在Rt△AME和Rt△BNE中
$\left\{\begin{array}{l}{AE=BE}\\{EM=EN}\end{array}\right.$
∴Rt△AME≌Rt△BNE(HL),
∴∠AEM=∠BEN,
∵∠ACB=90°,EM⊥AC,EN⊥BC,
∴∠CME=∠ACB=∠N=90°,
∴∠MEN=360°-3×90°=90°,
∴∠AEB=∠AEM+∠BEM=∠BEN+∠BEM=∠MEN=90°,
∵DE垂直平分AB,
∴ED=$\frac{1}{2}$AB,
同理CD=$\frac{1}{2}$AB,
∴CD=ED.
点评 本题考查了线段垂直平分线性质,角平分线性质,全等三角形的性质和判定的应用,能综合运用性质进行推理是解此题的关键,注意:线段垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.点(-5,y1)和点(-2,y2)都在一次函数y=-2x的图象上,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
8.一个数减去它的$\frac{1}{3}$等于$\frac{1}{4}$,则这个数为( )
| A. | $\frac{1}{6}$ | B. | $\frac{3}{8}$ | C. | 0 | D. | $\frac{7}{12}$ |
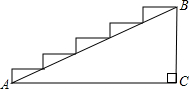 如图所示,在高为2m,坡度为30°的楼梯上铺地毯,已知地毯的单价为100元/米2,地毯宽为2m,求购此地毯的费用为多少?(结果保留整数)
如图所示,在高为2m,坡度为30°的楼梯上铺地毯,已知地毯的单价为100元/米2,地毯宽为2m,求购此地毯的费用为多少?(结果保留整数)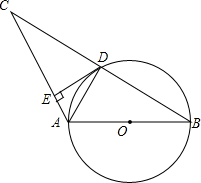 如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.
如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.