题目内容
20.某商场计划购进A、B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.(1)求A、B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900元,问最多能购进A种商品多少件?
分析 (1)设A两种商品的进价是a元,B两种商品的进价是b元,根据题意列方程组即可得到结论
(2)设购进A种商品x件,则购进B种商品(100-x)件,根据题意列不等式即可得到结论.
解答 解:(1)设A商品的进价是a元,B商品的进价是b元,
根据题意得:$\left\{\begin{array}{l}{20a+15b=380}\\{15a+10b=280}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=16}\\{b=4}\\{\;}\end{array}\right.$,
答:A商品的进价是16元,B商品的进价是4元;
(2)设购进A种商品x件,则购进B种商品(100-x)件,
根据题意得:16x+4(100-x)≤900,
解得:x≤41$\frac{2}{3}$,∵x为整数,
∴x的最大整数解为41,
∴最多能购进A种商品41件
点评 本题考查了二元一次方程组的应用,一元一次不等式的应用,正确的理解题意是解题的关键.

练习册系列答案
相关题目
11.已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AC}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ |
9.下列计算正确的是( )
| A. | (xy)3=xy3 | B. | x5÷x5=x | ||
| C. | 3x2•5x3=15x5 | D. | 5x2y3+2x2y3=10x4y9 |
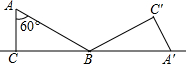 如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.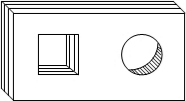 如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )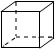


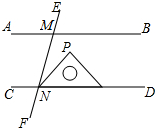
 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.
如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.