题目内容
5.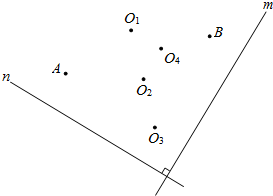 如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )
如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )| A. | O1 | B. | O2 | C. | O3 | D. | O4 |
分析 先根据点A、B的坐标求得直线AB的解析式,再判断直线AB在坐标平面内的位置,最后得出原点的位置.
解答 解:设过A、B的直线解析式为y=kx+b,
∵点A的坐标为(-4,2),点B的坐标为(2,-4),
∴$\left\{\begin{array}{l}{2=-4k+b}\\{-4=2k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
∴直线AB为y=-x-2,
∴直线AB经过第二、三、四象限,
如图,由A、B的坐标可知,沿CD方向为x轴正方向,沿CE方向为y轴正方向,
故将点A沿着CD方向平移4个单位,再沿着EC方向平移2个单位,即可到达原点位置,则原点为点O1.
故选:A.
点评 本题主要考查了坐标与图形性质,解决问题的关键是掌握待定系数法以及一次函数图象与系数的关系.在一次函数y=kx+b中,k决定了直线的方向,b决定了直线与y轴的交点位置.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
15.如果(4a2-3ab2)÷M=-4a+3b2,那么单项式M等于( )
| A. | ab | B. | -ab | C. | -a | D. | -b |
14. 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )| A. | 100° | B. | 72° | C. | 64° | D. | 36° |
 如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.
如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.
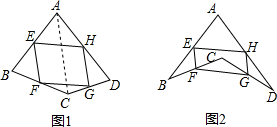
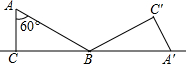 如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
如图,△ABC中,∠C=90°,∠A=60°,AB=2$\sqrt{3}$.将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是$\frac{5π}{2}$.
 如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.
如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=15°.