题目内容
15.若(m+1)x2+2mx-1=0是关于x的一元二次方程,则m的值是m≠-1.分析 一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.由这两个条件得到相应的关系式m+1≠0,再解不等式,进一步结合根的判别式判定即可.
解答 解:由题意得:m+1≠0,
解得:m≠-1,
且△=b2-4ac=4m2+4(m+1)=(2m+1)2+3>0,
方程始终有两个不相等的实数根.
故答案为:m≠-1.
点评 此题主要考查了一元二次方程的概念.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.以及根的判别式.

练习册系列答案
相关题目
3.已知x、y为实数,且y=$\sqrt{x-8}+\sqrt{8-x}-8$,则x-y的值是( )
| A. | -8 | B. | 0 | C. | 8 | D. | 16 |
20.将一根长1米的木棒,第一次截去一半,第二次截去剩下的一半,如此截下去,截至第五次,剩下的木棒长是( )米.
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
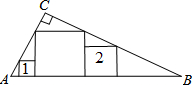 在Rt△ABC中,∠C=90°,现在其内部如图所示放置小、大、中三个正方形,其中小正方形边长为1,中正方形边长为2,则AC=$\frac{12\sqrt{5}}{5}$.
在Rt△ABC中,∠C=90°,现在其内部如图所示放置小、大、中三个正方形,其中小正方形边长为1,中正方形边长为2,则AC=$\frac{12\sqrt{5}}{5}$. 如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,求证:△ABM为等腰三角形.
如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,求证:△ABM为等腰三角形.