题目内容
6.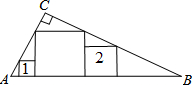 在Rt△ABC中,∠C=90°,现在其内部如图所示放置小、大、中三个正方形,其中小正方形边长为1,中正方形边长为2,则AC=$\frac{12\sqrt{5}}{5}$.
在Rt△ABC中,∠C=90°,现在其内部如图所示放置小、大、中三个正方形,其中小正方形边长为1,中正方形边长为2,则AC=$\frac{12\sqrt{5}}{5}$.
分析 根据题意可知△NFG∽△GCD∽△DEH,设DE=x,则GF=x+1,由$\frac{NF}{GF}=\frac{ED}{EH}$可求得x=1,然后再Rt△CGD和RtAMG中利用锐角三角函数的定义分别求得
AG和CG的长即可.
解答 解:如图所示;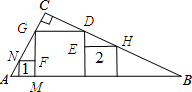
∵Rt△ABC中放置小、大、中三个正方形,
∴△NFG∽△GCD∽△DEH.
设DE=x,则GF=x+1.
∵△NFG∽△DEH,
∴$\frac{NF}{GF}=\frac{ED}{EH}$,即$\frac{1}{x+1}=\frac{x}{2}$.
解得:x=1或x=-2(舍去).
∴tan∠NGF=$\frac{1}{2}$.
∴sin∠NGF=$\frac{\sqrt{5}}{5}$,cos∠NGF=$\frac{2\sqrt{5}}{5}$.
∴AG=$\frac{GM}{cos∠AGM}$=$\frac{3}{\frac{2\sqrt{5}}{5}}$=$\frac{3}{2}\sqrt{5}$,GC=CD•sin∠CDG=3×$\frac{\sqrt{5}}{5}$=$\frac{3\sqrt{5}}{5}$.
∴AC=$\frac{3}{2}\sqrt{5}+\frac{3\sqrt{5}}{5}$=$\frac{21\sqrt{5}}{10}$.
故答案为:$\frac{21\sqrt{5}}{10}$.
点评 本题主要考查的是相似三角形的性质和判定,根据相似三角形的性质求得x的值是解题的关键.

练习册系列答案
相关题目
16.已知点P1(a,2013)和P2(-2012,b)关于原点对称,则(a+b)2014的值为( )
| A. | 1 | B. | -1 | C. | 72014 | D. | -72014 |
1. 如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
 如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )
如图,?ABCD中,E为AD的中点.已知△DEF的面积为1,则△BCF的面积为( )| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
11. 如图,△ABC≌△CDA,则BC的对应边是( )
如图,△ABC≌△CDA,则BC的对应边是( )
 如图,△ABC≌△CDA,则BC的对应边是( )
如图,△ABC≌△CDA,则BC的对应边是( )| A. | CD | B. | CA | C. | DA | D. | AB |