题目内容
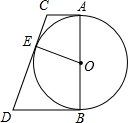 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.考点:切线的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:证明题
分析:连接OC、OD,如图,根据切线的性质得到OA⊥AC,OB⊥BD,而AC∥BD,则可判断点O、A、B共线,再利用切线的性质和切线长定理由CD切⊙O于点E得到
∴OE⊥CD,CE=CA,DE=DB,于是可根据角平分线的逆定理得CO平分∠AOE,DO平分∠BOE,则∠1=∠2,∠3=∠4,易得∠1+∠3=90°,即∠DOC=90°,
然后证明Rt△OCE∽Rt△DOE,利用相似比得CE•DE=OE2,所以AC•BD=OE2.
∴OE⊥CD,CE=CA,DE=DB,于是可根据角平分线的逆定理得CO平分∠AOE,DO平分∠BOE,则∠1=∠2,∠3=∠4,易得∠1+∠3=90°,即∠DOC=90°,
然后证明Rt△OCE∽Rt△DOE,利用相似比得CE•DE=OE2,所以AC•BD=OE2.
解答: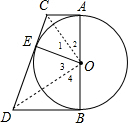 证明:连接OC、OD,如图,
证明:连接OC、OD,如图,
∵AC,BD是⊙O的两条切线,A,B为切点,
∴OA⊥AC,OB⊥BD,
∵AC∥BD,
∴OA⊥BD,
∴点O、A、B共线,即AB为⊙O的直径,
∵CD切⊙O于点E,
∴OE⊥CD,CE=CA,DE=DB,
∴CO平分∠AOE,DO平分∠BOE,
∴∠1=∠2,∠3=∠4,
而∠1+∠2+∠3+∠4=180°,
∴∠1+∠3=90°,即∠DOC=90°,
∵∠3+∠ODE=90°,
∴∠1=∠ODE,
∴Rt△OCE∽Rt△DOE,
∴CE:OE=OE:DE,
∴CE•DE=OE2,
∴AC•BD=OE2,
而OE为⊙O的半径,
∴AC•BD为定值.
 证明:连接OC、OD,如图,
证明:连接OC、OD,如图,∵AC,BD是⊙O的两条切线,A,B为切点,
∴OA⊥AC,OB⊥BD,
∵AC∥BD,
∴OA⊥BD,
∴点O、A、B共线,即AB为⊙O的直径,
∵CD切⊙O于点E,
∴OE⊥CD,CE=CA,DE=DB,
∴CO平分∠AOE,DO平分∠BOE,
∴∠1=∠2,∠3=∠4,
而∠1+∠2+∠3+∠4=180°,
∴∠1+∠3=90°,即∠DOC=90°,
∵∠3+∠ODE=90°,
∴∠1=∠ODE,
∴Rt△OCE∽Rt△DOE,
∴CE:OE=OE:DE,
∴CE•DE=OE2,
∴AC•BD=OE2,
而OE为⊙O的半径,
∴AC•BD为定值.
点评:本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径.也考查了切线长定理、角平分线定理的逆定理和相似三角形的判定与性质.

练习册系列答案
相关题目
方程3-
=-
,去分母得( )
| 5x+7 |
| 2 |
| x+17 |
| 4 |
| A、3-2(5x+7)=-(x+17) |
| B、12-(5x+7)=-x+17 |
| C、12-(5x+7)=-(x+17) |
| D、12-10x+14=-(x+17) |
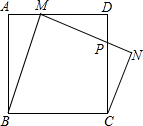 如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=
如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=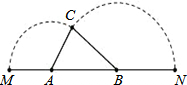 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC为直角三角形,则x=
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC为直角三角形,则x=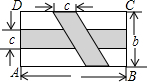 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是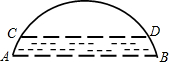 如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧
如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧
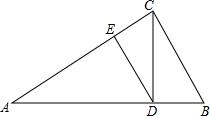 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC.