题目内容
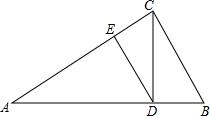 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC.(1)图中有几对相似三角形,请写出来.
(2)请选择其中的一对给予证明.
考点:相似三角形的判定
专题:
分析:(1)由在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC,以及公共角,根据有两组角对应相等的两个三角形相似,即可证得△ADE∽△DCE∽△CBD∽△ACD∽△ABC;
(2)由在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC,可得∠AED=ACB=90°,又由∠A是公共角,即可证得△ADE∽△ABC.
(2)由在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC,可得∠AED=ACB=90°,又由∠A是公共角,即可证得△ADE∽△ABC.
解答:解:(1)∵在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC,
∴∠AED=ACB=90°,
∵∠A是公共角,
∴△ADE∽△ABC,
同理:△BCD∽△BAC,△ACD∽△ABC,△CDE∽△CAD,
∴△ADE∽△DCE∽△CBD∽△ACD∽△ABC,
∴图中有10对相似三角形.
(2)选择△ADE∽△ABC,
证明:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC,
∴∠AED=ACB=90°,
∵∠A是公共角,
∴△ADE∽△ABC.
∴∠AED=ACB=90°,
∵∠A是公共角,
∴△ADE∽△ABC,
同理:△BCD∽△BAC,△ACD∽△ABC,△CDE∽△CAD,
∴△ADE∽△DCE∽△CBD∽△ACD∽△ABC,
∴图中有10对相似三角形.
(2)选择△ADE∽△ABC,
证明:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,DE⊥AC,
∴∠AED=ACB=90°,
∵∠A是公共角,
∴△ADE∽△ABC.
点评:此题考查了相似三角形的判定以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a:b:c=
:
:
,则a:b:c化为整数比为( )
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| A、3:4:5 |
| B、5:4:3 |
| C、20:15:12 |
| D、12:15:20 |
下列命题:①同旁内角互补,两直线平行:②全等三角形的周长相等;③直角都相等;④相等的角是对项角.它们的逆命题是真命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
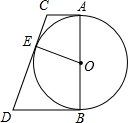 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.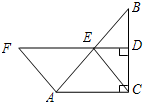 如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.
如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.