题目内容
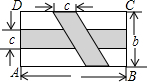 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是(用含c的代数式表示)
考点:矩形的性质,平行四边形的性质
专题:
分析:根据题中图形,空白部分面积实际上是一个长为(a-c),宽为(b-c)的新矩形,按照面积公式计算即可.
解答:解:本题中空白部分的面积=矩形ABCD的面积-阴影部分的面积.
矩形ABCD的面积为:a×b=ab;
阴影部分的面积为:a×c+b×c-c×c=ac+bc-c2;
那么空白部分的面积为:ab-ac-bc+c2;
因为a=2b=6c,
所以ab-ac-bc+c2
=6c•3c-6c•c-3c•c+c2
=18c2-6c2-3c2+c2
=10c2.
故答案为10c2.
矩形ABCD的面积为:a×b=ab;
阴影部分的面积为:a×c+b×c-c×c=ac+bc-c2;
那么空白部分的面积为:ab-ac-bc+c2;
因为a=2b=6c,
所以ab-ac-bc+c2
=6c•3c-6c•c-3c•c+c2
=18c2-6c2-3c2+c2
=10c2.
故答案为10c2.
点评:本题考查了矩形的性质,平行四边形的性质,要注意图片给出的信息,要特别注意阴影中重叠部分的面积不要丢掉.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在代数式中2x3,-ab2,13xyz,8πr2是三次单项式的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若a:b:c=
:
:
,则a:b:c化为整数比为( )
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| A、3:4:5 |
| B、5:4:3 |
| C、20:15:12 |
| D、12:15:20 |
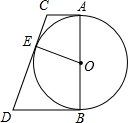 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
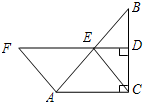 如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.
如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.