题目内容
某学校欲招一名语文教师,对甲、乙、丙三名候选人进行了三项素质测试,她们的各项测试成绩如表所示:
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,学校将课堂教学、普通话和粉笔字三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,学校将课堂教学、普通话和粉笔字三项测试得分按4:3:1的比例确定各人的测试成绩,此时谁将被录用?
| 测试项目 | 测试成绩 | ||
| 甲 | 乙 | 丙 | |
| 课堂教学 | 74 | 87 | 69 |
| 普通话 | 58 | 74 | 70 |
| 粉笔字 | 87 | 43 | 65 |
考点:加权平均数,算术平均数
专题:
分析:(1)根据平均数的计算方法是求出所有数据的和,然后除以数据的总个数,求出甲、乙、丙的平均成绩再进行比较即可,
(2)根据加权平均数的计算公式和每一部分所占的权求出各人的测试成绩,再进行比较即可.
(2)根据加权平均数的计算公式和每一部分所占的权求出各人的测试成绩,再进行比较即可.
解答:解:(1)∴甲的平均成绩为:
(74+58+87)=73(分)
乙的平均成绩为:
(87+74+43)=68(分)
丙的平均成绩为:
(69+70+65)=68(分)
∴根据三项测试的平均成绩确定录用人选,那么甲将被录用;
(2)将课堂教学、普通话和粉笔字三项测试得分按4:3:1的比例确定各人的测试成绩,
此时甲的测试成绩为:
=69.625(分),
乙的测试成绩为:
=76.625(分),
丙的测试成绩为:
=68.875(分),
则此时乙将被录用.
| 1 |
| 3 |
乙的平均成绩为:
| 1 |
| 3 |
丙的平均成绩为:
| 1 |
| 3 |
∴根据三项测试的平均成绩确定录用人选,那么甲将被录用;
(2)将课堂教学、普通话和粉笔字三项测试得分按4:3:1的比例确定各人的测试成绩,
此时甲的测试成绩为:
| 74×4+58×3+87 |
| 8 |
乙的测试成绩为:
| 87×4+74×3+43 |
| 8 |
丙的测试成绩为:
| 69×4+70×3+65 |
| 8 |
则此时乙将被录用.
点评:本题考查的是加权平均数的求法,用到的知识点是平均数和加权平均数的计算公式,关键是根据公式列出算式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
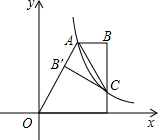 如图,双曲线y=
如图,双曲线y=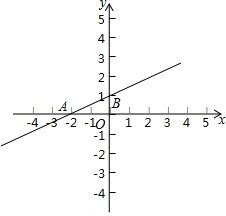 如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).
如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).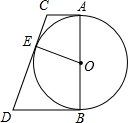 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.