题目内容
(1)解方程:
=
(2)解不等式组
并把解集在数轴上表示出来.
(3)先化简,再求值:(
-
)÷
,其中x=1.
| 5 |
| x+1 |
| 4 |
| x-3 |
(2)解不等式组
|
(3)先化简,再求值:(
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
考点:分式的化简求值,解分式方程,在数轴上表示不等式的解集,解一元一次不等式组
专题:
分析:(1)根据解分式方程的步骤计算即可.
(2)分别求得各不等式的集,求得公共解集,然后在数轴上表示即可.
(3)先化简(
-
)÷
,得到
-
,把x=1代入即可求得代数式的值.
(2)分别求得各不等式的集,求得公共解集,然后在数轴上表示即可.
(3)先化简(
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
| 1 |
| 2 |
| x |
| 2(x-2) |
解答:解:(1)
=
,
去分母,得5(x-3)=4(x+1),
去括号,得,5x-15=4x+4
移项合并同类项,得,x=19
经经验,x=19是原方程的根.
(2)
解不等式①得,x<5,
解不等式②得,x≥3,
所以不等式组的解集为3≤x<5.
在数轴上表示为:
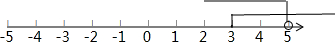
(3)原式=
×
-
×
=
-
当x=1时,
原式=
-
=
+
=1
| 5 |
| x+1 |
| 4 |
| x-3 |
去分母,得5(x-3)=4(x+1),
去括号,得,5x-15=4x+4
移项合并同类项,得,x=19
经经验,x=19是原方程的根.
(2)
|
解不等式①得,x<5,
解不等式②得,x≥3,
所以不等式组的解集为3≤x<5.
在数轴上表示为:
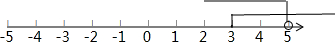
(3)原式=
| 1 |
| x(x-2) |
| x(x-2) |
| 2 |
| 1 |
| (x-2)2 |
| x(x-2) |
| 2 |
=
| 1 |
| 2 |
| x |
| 2(x-2) |
当x=1时,
原式=
| 1 |
| 2 |
| 1 |
| 2(1-2) |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了解分式方程,解不等式组,分式的化简求值,要注意它们的运算顺序和步骤.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在代数式中2x3,-ab2,13xyz,8πr2是三次单项式的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
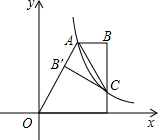 如图,双曲线y=
如图,双曲线y=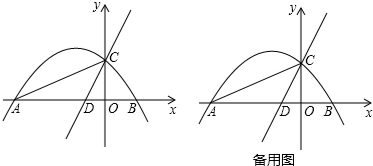
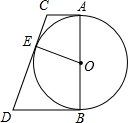 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.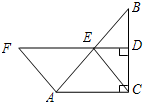 如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.
如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.