题目内容
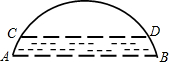 如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧
如图是一座桥其中一个拱洞的简易图形,最初的水位在AB处,此时水面宽60米,拱高(拱弧 |
| AB |
考点:垂径定理的应用,勾股定理
专题:
分析:由GE为弓形AB的高,得弧AB的圆心在直线GE上,设圆心为O,连OC,OA,AB=60m,GE=10m,则AE=BE=30m,FE=5m,在Rt△OAE中,利用勾股定理求出半径,再在Rt△OCF中,利用勾股定理计算出CF,则CD=2CF.
解答: 解:∵GE为弓形AB的高,
解:∵GE为弓形AB的高,
∴弧AB的圆心在直线GE上,
设圆心为O,连OC,OA,如图,由题意,得AB=60m,GE=10m,
根据题意得,AE=BE=30m,FE=5m,GF=5m
设圆的半径为R,
在Rt△OAE中,∵∠OEA=90°,OE=R-10,
∴R2=302+(R-10)2,
解得,R=50,
在Rt△OCF中,∵∠OFC=90°,OC=50m,OF=45m,
∴CF=
=
=5
(m),
∴CD=2CF=10
m.
即此时的水面CD的宽度为10
m.
 解:∵GE为弓形AB的高,
解:∵GE为弓形AB的高,∴弧AB的圆心在直线GE上,
设圆心为O,连OC,OA,如图,由题意,得AB=60m,GE=10m,
根据题意得,AE=BE=30m,FE=5m,GF=5m
设圆的半径为R,
在Rt△OAE中,∵∠OEA=90°,OE=R-10,
∴R2=302+(R-10)2,
解得,R=50,
在Rt△OCF中,∵∠OFC=90°,OC=50m,OF=45m,
∴CF=
| OC2-OF2 |
| 502-452 |
| 19 |
∴CD=2CF=10
| 19 |
即此时的水面CD的宽度为10
| 19 |
点评:本题考查了垂径定理的应用,勾股定理,难度适中.求出
所在圆的半径是解题的关键.
 |
| AB |

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
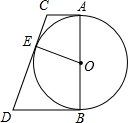 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
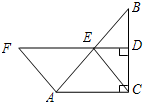 如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.
如图,在Rt△ABC中,∠ACB=90°,点E为AB中点,连结CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE.