题目内容
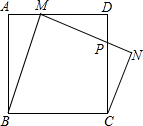 如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=
如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=考点:正方形的性质,勾股定理,等腰梯形的性质
专题:
分析:作BG⊥MN于G,连接BP,由于等腰梯形BMNC,得出∠BMN=∠MBC,由AD∥BC得出∠AMB=∠MBC,即可得出∠AMB=∠NMB,由BA⊥AM,BG⊥MN根据角的平分线的性质得出BA=BG,根据AB=1,AM=x,CP=y,得出GP=CP=y,MD=1-x,PD=1-y,最后根据勾股定理得出(1-x)2+(1-y)2=(x+y)2就可以得出y关于x的函数关系式.
解答: 解:如图,作BG⊥MN于G,连接BP.
解:如图,作BG⊥MN于G,连接BP.
∵等腰梯形BMNC,其中BM∥MN,
∴∠BMN=∠MBC,
∵AD∥BC,
∴∠AMB=∠MBC,
∴∠AMB=∠NMB,
∵BA⊥AM,BG⊥MN,
∴BA=BG,
∴AM=GM=x,
∴BC=BG,
∴GP=CP=y,
MD=1-x,PD=1-y,
∴(1-x)2+(1-y)2=(x+y)2,
∴xy+x+y=1,
∴y=
(0<x<1).
故答案为
(0<x<1).
 解:如图,作BG⊥MN于G,连接BP.
解:如图,作BG⊥MN于G,连接BP.∵等腰梯形BMNC,其中BM∥MN,
∴∠BMN=∠MBC,
∵AD∥BC,
∴∠AMB=∠MBC,
∴∠AMB=∠NMB,
∵BA⊥AM,BG⊥MN,
∴BA=BG,
∴AM=GM=x,
∴BC=BG,
∴GP=CP=y,
MD=1-x,PD=1-y,
∴(1-x)2+(1-y)2=(x+y)2,
∴xy+x+y=1,
∴y=
| 1-x |
| 1+x |
故答案为
| 1-x |
| 1+x |
点评:本题考查了正方形的性质,等腰梯形的性质,角的平分线的性质,勾股定理的应用等,角的平分线性质定理的应用是本题的关键.

练习册系列答案
相关题目
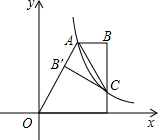 如图,双曲线y=
如图,双曲线y=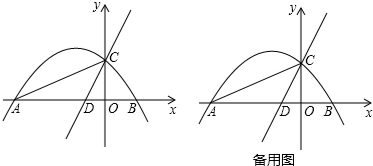
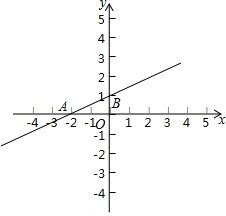 如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).
如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).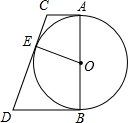 如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.
如图,已知AC,BD是半径为R的圆的两条平行切线,A,B为切点,CD切⊙O于点E,交AC于点C,交BD于点D,求证:AC•BD为定值.