题目内容
已知△ABC∽△DEF,且AB=2DE,h1,h2分别为AB、DE边上的高线,则
=( )
| h1 |
| h2 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
考点:相似三角形的性质
专题:
分析:由条件可求得相似比,再利用相似三角形对应边上的比等于相似比可得出答案.
解答:解:
∵△ABC∽△DEF,h1,h2分别为AB、DE边上的高线,
∴
=
,
∵AB=2DE,
∴
=2,
故选A.
∵△ABC∽△DEF,h1,h2分别为AB、DE边上的高线,
∴
| h1 |
| h2 |
| AB |
| DE |
∵AB=2DE,
∴
| h1 |
| h2 |
故选A.
点评:本题主要考查相似三角形的性质,掌握相似三角形对应边上的高的比等于相似比是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x1和x2是方程x2-x-1=0的两个根,则x12+x1x2+x22的值是( )
| A、1 | B、2 | C、3 | D、-1 |
下列运算结果正确的是( )
| A、x3+x3=x4 |
| B、(x3)2=x5 |
| C、x3+x4=x2 |
| D、x•x3=x4 |
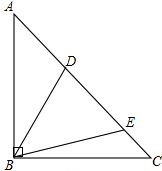 如图,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=
如图,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=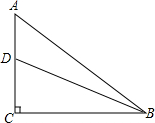 如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=
如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=