题目内容
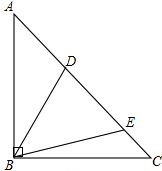 如图,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=
如图,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE=| 1 |
| 2 |
考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:证明题
分析:把△CBE逆时针旋转90°,根据已知条件证明DE=DE′,由于△ABC是等腰直角三角形,故可知图形旋转后点C与点A重合,∠E′AB=∠BCE=45°,所以∠DAE′=90°,再根据勾股定理即可得出结论.
解答:证明:如图所示:把△CBE逆时针旋转90°,连接DE′,
∵∠DBE=
∠ABC,
∴∠ABD+∠CBE=∠DBE=
∠ABC,
∵△ABE′由△CBE旋转而成,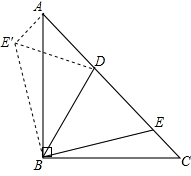
∴BE=BE′,∠ABE′=∠CBE,
∴∠DBE′=∠DBE,
在△DBE与△DBE′中,
,
∴△DBE≌△DBE′,
∴DE′=DE,
∵BA=BC,∠ABC=90°,
∴∠BAC=∠BCE=45°,
∴图形旋转后点C与点A重合,CE与AE′重合,
∴AE′=EC,
∴∠E′AB=∠BCE=45°,
∴∠DAE′=90°,
在Rt△ADE′中,DE′2=AE′2+AD2,
∵AE′=EC,
∴DE′2=EC2+AD2,
∵DE=DE′,
∴DE′2=AD2+EC2,
∴DE2=AD2+EC2.
∵∠DBE=
| 1 |
| 2 |
∴∠ABD+∠CBE=∠DBE=
| 1 |
| 2 |
∵△ABE′由△CBE旋转而成,

∴BE=BE′,∠ABE′=∠CBE,
∴∠DBE′=∠DBE,
在△DBE与△DBE′中,
|
∴△DBE≌△DBE′,
∴DE′=DE,
∵BA=BC,∠ABC=90°,
∴∠BAC=∠BCE=45°,
∴图形旋转后点C与点A重合,CE与AE′重合,
∴AE′=EC,
∴∠E′AB=∠BCE=45°,
∴∠DAE′=90°,
在Rt△ADE′中,DE′2=AE′2+AD2,
∵AE′=EC,
∴DE′2=EC2+AD2,
∵DE=DE′,
∴DE′2=AD2+EC2,
∴DE2=AD2+EC2.
点评:本题考查的是图形的旋转及勾股定理以及全等三角形的判定和性质,熟知旋转前、后的图形全等是解答此题的关键.题目的综合性较强,难度不小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以下四个图中对称轴条数最多的一个图形是( )
A、 |
B、 |
C、 |
D、 |
已知△ABC∽△DEF,且AB=2DE,h1,h2分别为AB、DE边上的高线,则
=( )
| h1 |
| h2 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
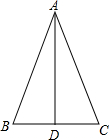 如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.
如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.